澳门威斯尼斯615人官方
“信息与计算科学”专业课程教学大纲
培养方案修订负责人:陆书环 教学大纲统稿人:王利广
数学分析教学大纲
教研室主任:张克梅 执笔人:孙钦福
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数学分析
课程编号:06200131
英文名称:Mathematical Analysis
课程类型:专业基础课
总 学 时:289 理论学时: 289 实验学时:0 课外学时:0
学 分:17
开设专业:信息与计算科学
先修课程:无
二、课程任务目标
(一)课程任务
本课程是数学系的一门重要基础课,其主要任务是使学生获得数学的基本思想方法和极限论、单元与多元微积分、级数论、广义积分等方面的系统知识。它一方面为后继课程(如《微分方程》、《实变函数》、《复变函数》、《概率论与统计学》及有关的《泛函分析》、《微分几何》等限选课程及《普通物理》等)提供一些所需的基础理论和知识,另一方面还对提高学生思维能力,开发学生智能加强“三基”(基础知识、基本理论、基本技能)及培养学生独立工作能力等起着重要的作用。
(二)课程目标
通过本课程教学的主要环节(讲授与讨论、习题课、作业、辅导等),使学生对极限思想和方法有较深的认识和理解,从而有助于培养学生辩证唯物主义基本观点及正确理解《数学分析》的基本概念和论证方法及分析问题和解决问题的能力。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 实数集与函数
1、理解函数的概念,掌握函数的表示方法,并会建立简单应用问题中的函数关系式。
2、了解函数的奇偶性、单调性、周期性和有界性。
3、理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4、掌握基本初等函数的性质及其图形。
5.理解确界概念,并会证明确界原理。
第二章 数列极限
1.理解数列极限的概念,并会应用“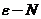 ”语言证明数列极限。
”语言证明数列极限。
2.掌握收敛数列的性质,并会利用收敛数列的性质证明数列的有关问题。
3.掌握数列极限存在的条件,并会应用单调有界定理证明数列极限存在,会应用柯西收敛准则证明数列收敛与发散。
4.掌握数列极限的否定定义,并会应用。
第三章 函数极限
1.理解函数极限的概念,理解函数左极限与右极限的概念,以及极限存在与左、右极限之间的关系,并会应用定义证明函数在各种极限过程下的极限。
2.掌握各种情形下函数极限的否定定义,并会用否定定义证明问题。
3.掌握函数极限的性质及四则运算法则,并会证明。
4.掌握函数极限存在的两个准则(归结原则与柯西准则),并会利用它们求极限,掌握利用两个重要极限求极限的方法。
5.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限。
第四章 函数的连续性
1.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。
2.掌握连续函数的性质和初等函数的连续性,会证明闭区间上连续函数的性质(有界性定理、最大值和最小值定理、介值定理、反函数的连续性定理、一致连续性定理),并会应用这些性质。
第五章 导数与微分
1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系。
2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式。理解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分。
3、理解高阶导数与高阶微分的概念,会求简单函数的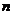 阶导数与
阶导数与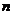 阶微分。
阶微分。
4、会求分段函数的一阶、二阶导数。
5、会求隐函数和由参数方程所确定的函数的一阶、二阶导数,会求反函数的导数。
第六章 微分中值定理及其应用
1.理解并会用洛尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理,并会应用它们证明问题。
2.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其简单应用。
3.会用导数判断函数图形的凹凸性,会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形。
4.掌握用洛必达法则求未定式极限的方法。
第七章 实数的完备性
1.掌握实数完备性的基本定理的证明,并会证明它们的等价性。
2.掌握闭区间上连续函数性质的证明,并会应用它们解决其他问题。
3.理解上极限和下极限的概念及性质,并会求数列的上下极限。
第八章 不定积分
1.理解原函数概念,理解不定积分的概念。
2.掌握不定积分的基本公式,掌握不定积分的性质,掌握换元积分法与分部积分法。
3.会求有理函数、三角函数有理式和简单无理函数的积分。
第九章 定积分
1.理解定积分的概念。
2.掌握牛顿莱布尼兹公式,会用定积分求数列的极限。
3.掌握定积分存在的必要条件和充要条件,并会应用它们证明一些分析问题。
4.掌握定积分的性质并会灵活运用。
5.理解变上限定积分定义的函数,会求它的导数,掌握微积分基本定理,并会证明。
6.理解积分第二中值定理,并会应用。
7.掌握换元积分法与分部积分法。
8.了解大和与小和的概念
第十章 定积分的应用
1.掌握用定积分表达和计算一些几何量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积)。
2.了解曲率和曲率半径的概念,会计算曲率和曲率半径。
3.了解定积分在物理上的某些应用(变力做功、引力、压力和函数的平均值等)。
第十一章 反常积分
1.了解两类反常积分的概念并会计算两类反常积分。
2.会用定义判断反常积分的收敛与发散。
3.掌握无穷积分与暇积分的性质以及收敛性判别方法(比较判别法,柯西判别法,狄里克莱判
别法与阿贝尔判别法)。
4.掌握无穷积分的绝对收敛与条件收敛的概念。
第十二章 数项级数
1.理解数项级数收敛、发散以及收敛级数和的概念,掌握级数的基本性质及收敛的必要条件。
2.掌握几何级数与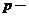 级数的收敛与发散的条件。
级数的收敛与发散的条件。
3.掌握正项级数收敛性判别法(比较判别法、比式判别法、根式判别法、积分判别法以及拉贝判别法)。
4.掌握交错级数的莱布尼兹判别法。
5.理解任意项级数绝对收敛与条件收敛的概念,以及绝对收敛级数与收敛级数的关系,理解绝对收敛级数的性质。
6.掌握一般项级数的阿贝尔判别法与狄里克莱判别法。
第十三章 函数列与函数项级数
1.熟练掌握函数列与函数项级数的一致收敛与非一致收敛的定义,并会证明函数列与函数项级数的一致收敛与非一致收敛。
2.掌握判别函数列与函数项级数的一致收敛与非一致收敛的方法。
3.掌握一致收敛函数列与函数项级数的性质(连续性、可积性、可微性),并会熟练这些定理的证明以及应用。
第十四章 幂级数
1.理解幂级数收敛半径的概念,并掌握幂级数的收敛半径、收敛区间及收敛域的求法。
2.理解幂级数在其收敛区间内的一些基本性质(和函数的连续性、逐项微分和逐项积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些数项级数的和。
3.了解函数展开为泰勒级数的充分必要条件。
4.掌握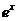 、
、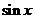 、
、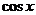 、
、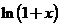 、
、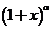 的麦克劳林展开式,会用它们将一些简单函数间接展开成幂级数。
的麦克劳林展开式,会用它们将一些简单函数间接展开成幂级数。
5.了解复变量的指数函数及欧拉公式。
第十五章 傅里叶级数
1.了解傅里叶级数的概念和函数展开为傅里叶级数的收敛定理。
2.会将定义在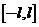 上的函数展开为傅里叶级数,会将定义在
上的函数展开为傅里叶级数,会将定义在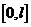 上的函数展开为正弦级数与
上的函数展开为正弦级数与
余弦级数,会写出傅里叶级数的和的表达式。
3.了解傅里叶级数收敛定理的证明。
第十六章 多元函数的极限与连续
1.理解平面点集的一些基本概念,了解多元函数的概念,理解二元函数的几何意义。
2.掌握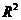 上的完备性定理,并会应用。
上的完备性定理,并会应用。
3.理解二元函数极限的概念,并会应用定义证明二元函数的极限。
4.掌握重极限与累次极限之间的关系。
5.理解二元函数连续性的概念以及有界闭区域上连续函数的性质,并会证明与应用。
第十七章 多元函数微分学
1.理解多元函数偏导数和全微分的概念,会求偏导数与全微分,理解可微的必要条件与充分条
件存在的必要条件和充分条件,了解偏导数与全微分的几何意义。
2.掌握多元复合函数偏导数与全微分的求法,理解一阶全微分形式的不变性。
3.理解方向导数与梯度的概念并掌握其计算方法。
4.掌握高阶偏导数的求法,混合偏导数与求导顺序无关定理。
5.了解二元函数的中值定理与泰勒公式。
6.理解多元函数极值的概念,掌握多元函数极值存在的必要条件,二元函数极值存在的充分条
件,会求二元函数的极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题。
第十八章 隐函数定理及其应用
1.了解隐函数的概念,掌握隐函数存在唯一性定理与隐函数可微性定理,会求隐函数的偏导数
及高阶偏导数。
2.了解隐函数组的概念,掌握隐函数组存在唯一性定理与可微性定理,会求隐函数组确定的隐
函数的偏导数及高阶偏导数。
3.了解反函数组定理。
4.了解曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程。
5.理解多元函数条件极值的概念,掌握用拉格朗日乘数法求条件极值,会求简单多元函数的最
大值和最小值,并会解决一些简单的应用问题。
第十九章 含参量积分
1.理解含参量正常积分的概念,掌握含参量积分的连续性、可微性、可积性。
2.掌握含参量反常积分的一致收敛性及其判别法,掌握含参量反常积分的分析性质,并会应用
这些性质计算含参量积分。
3.掌握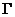 函数与
函数与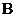 函数的定义以及它们之间的关系,并会应用
函数的定义以及它们之间的关系,并会应用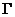 函数与
函数与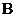 函数计算一些积分。
函数计算一些积分。
第二十章 曲线积分
1.理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系。
2.掌握计算两类曲线积分的方法。
第二十一章 重积分
1.理解二重积分、三重积分的概念,了解重积分的性质,了解二重积分的中值定理。
2.掌握二重积分的计算方法(直角坐标、极坐标),会计算三重积分(直角坐标、柱面坐标、球面坐标)。
3.掌握格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数。
4.了解二重积分的变量变换公式。
5.会求曲面的面积,物体的重心、转动惯量。
6.了解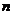 重积分的概念,会计算反常二重积分,了解在一般条件下重积分变量变换公式的证明。
重积分的概念,会计算反常二重积分,了解在一般条件下重积分变量变换公式的证明。
第二十二章 曲面积分
1.了解两类曲面积分的概念、性质及两类曲面积分的关系,掌握计算两类曲面积分的方法,会用高斯公式、斯托克斯公式计算曲面、曲线积分。
2.了解散度与旋度的概念,并会计算。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 实数集与函数 |
10 |
8 |
|
|
2 |
|
|
|
第二章 数列极限 |
16 |
12 |
|
|
4 |
|
|
|
第三章 函数极限 |
16 |
12 |
|
|
4 |
|
|
|
第四章 函数的连续性 |
18 |
12 |
|
|
6 |
|
|
|
第五章 导数与微分 |
14 |
10 |
|
|
4 |
|
|
|
第六章 微分中值定理及其应用 |
18 |
12 |
|
|
6 |
|
|
|
第七章 实数的完备性 |
10 |
6 |
|
|
4 |
|
|
|
第八章 不定积分 |
12 |
8 |
|
|
4 |
|
|
|
第九章 定积分 |
22 |
16 |
|
|
6 |
|
|
|
第十章 定积分的应用 |
10 |
8 |
|
|
2 |
|
|
|
第十一章 反常积分 |
12 |
8 |
|
|
4 |
|
|
|
第十二章 数项级数 |
12 |
8 |
|
|
4 |
|
|
|
第十三章 函数列与函数项级数 |
14 |
10 |
|
|
4 |
|
|
|
第十四章 幂级数 |
10 |
8 |
|
|
2 |
|
|
|
第十五章 傅里叶级数 |
10 |
8 |
|
|
2 |
|
|
|
第十六章 多元函数的极限与连续 |
10 |
8 |
|
|
2 |
|
|
|
第十七章 多元函数微分学 |
14 |
10 |
|
|
4 |
|
|
|
第十八章 隐函数定理及其应用 |
10 |
8 |
|
|
2 |
|
|
|
第十九章 含参量积分 |
14 |
10 |
|
|
4 |
|
|
|
第二十章 曲线积分 |
8 |
6 |
|
|
2 |
|
|
|
第二一章 重积分 |
16 |
12 |
|
|
4 |
|
|
|
第二二章 曲面积分 |
13 |
9 |
|
|
4 |
|
|
|
第二三章 流形上微积分学初阶 |
0 |
0 |
|
|
0 |
|
|
|
合计 |
289 |
209 |
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+其中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1. 华东师范大学数学系编 《数学分析》,高等教育出版社,2001年。
(二)主要参考书目
1.刘一鸣、周家云、解际太,《数学分析》,山东大学出版社,93年版。
2.刘立山、孙钦福,《数学分析的基本理论与典型方法》,中国科学技术出版社,05年版。
“高等代数”教学大纲
教研室主任:王培合 执笔人:彭桢
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:高等代数
课程编号: 06200221
英文名称:Advanced Algebra
课程类型:专业基础课
总 学 时: 187 理论学时:187 实验学时:0 课外学时:0
学 分: 11
开设专业:信息与计算科学
先修课程:无
二、课程任务目标
(一)课程任务
本课程是一门数学专业本科生重要的基础课,是数学专业本专科生学习其他后继科目的基础。其主要任务是传授给学生代数思想方法及多项式和线性代数的基本知识。《高等代数》为学生进一步学习与研究代数,几何及其它方向提供了基础知识,基本技能,基本理论并充分展示了代数学的思维特点。通过本课程的学习,应使学生掌握多项式特别是线性代数的基本概念、性质及一些经典结论,最重要的是,使学生能够灵活运用代数学思维方法和技巧。
(二)课程目标
在学完本课程之后,学生能够:
1.正确理解和掌握数域、多项式的相关的概念,掌握多项式运算。
2.利用带余除法,辗转相除法求两多项式的商和余式以及最大公因式。
3.应用余数定理求值,并进行实、复系数多项式的因式分解。
4.判断有理系数多项式是否为本原多项式,不可约多项式并进行适当的因式分解。
5.了解多元多项式的有关概念性质和对称多项式基本定理。
6.灵活利用各种方法对行列式进行简化并计算。
7.利用克兰姆(Cramer)法则求解线性方程组,并认识拉普拉斯(Laplace)定理和行列式的乘法规则。
8.掌握线性方程组的高斯消元法。
9.求任意n维向量组的线性相关(无关)性,求向量组的极大线性无关组并用极大线性无关组线性表出其他向量。
10.求矩阵的秩,并能应用矩阵的秩。
11.判定(齐次)线性方程组是否有(非零)解,描述线性方程组解的结构,并能熟练求解线性方程组。
12.了解求解二元高次方程组的一般方法。
13.计算矩阵的和、差、乘积、数量乘积、转置、方幂、可逆矩阵的逆、矩阵乘积的行列式和矩阵乘积的秩。
14.求任意方阵的伴随矩阵,并研究伴随矩阵与原矩阵的关系。
15.利用初等矩阵的性质、矩阵的初等变换、可逆矩阵的分解以及分块矩阵的运算、初等变换研究矩阵的性质。
16.了解广义逆矩阵的性质求解矩阵方程。
17.通过非退化的线性替换把二次型[对称矩阵]化简为标准形[对角矩阵]。
18.掌握复、实系数二次型的规范形的唯一性及理论推导,理解并能熟练应用(半)正定二次型[矩阵]的定义、性质及判定,总结出矩阵的合同不变性质。
19.熟练应用非退化线性替换及矩阵的合同变换化简二次型、对称矩阵成标准形或规范形,应用二次型[对称矩阵]的有关理论于某些等式或不等式的证明。
20.计算线性空间的维数和基,通过不同基之间的变换求向量的坐标。
21.通过现行变换和矩阵的关系,利用矩阵简化线性变换。
22.求矩阵的特征值和特征向量,并利用特征向量化矩阵为若而当标准形。
23.通过内积的定义区别欧式空间和线性空间,并掌握正交变换和正交阵的关系。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 多项式
第一节 数域
1.掌握数域的概念;
2.理解有理数数域是最小的数域,掌握复数域,实数域和有理数域之间的关系。
第二节 一元多项式
1.了解一元多项式的定义;
2.掌握一元多项式的四则运算及其性质。
第三节 整除的概念
1.掌握带余除法定理,并利用带余除法定理计算商和余式;
2.理解整除的概念,掌握整除的判定。
3.掌握综合除法。
第四节 最大公因式
1.理解最大公因式的概念;
2.掌握辗转相除法,并会求满足要求的 ;
;
3.理解互素的概念,掌握互素的判定方法。
第五节 因式分解定理
1.掌握不可约多项式的概念及性质;
2.理解因式分解及唯一性定理;,掌握多项式的标准分解式。
第六节 重因式
1.掌握k重因式的概念,理解重因式与微商的关系。
第七节 多项式函数
1.掌握余数定理及其推论;
2.理解多项式函数和多项式之间的关系。
第八节 复系数与实系数多项式的因式分解
1.掌握代数学基本定理;
2.理解复系数多项式因式分解定理,掌握复系数多项式的标准分解式。
2.理解实系数多项式因式分解定理,掌握实系数多项式的标准分解式。
第九节 有理系数多项式
1.掌握本元多项式的概念;
2.理解高斯引理,掌握有理系数多项式的基本性质以及埃森斯坦因判别法。
第十节 多元多项式
1.掌握多元多项式以及对称多项式的概念,并利用带余除法定理计算商和余式;
2.理解对称多项式的基本定理,掌握多元多项式的因式分解和简化。
第二章 行列式
第一节 引言
1.掌握二阶和三阶行列式的算法理解行列式与线性方程组的关系。
第二节 排列
1.掌握排列,逆序数,奇偶排列的概念;
2.理解排列的奇偶性与置换的关系。
第三节 n级行列式
1.了解利用定义计算行列式的方法;
2.掌握行列式的性质1。
第四节 n级行列式的性质
1.理解并掌握行列式的各种性质。
第五节 行列式的计算
1.理解矩阵的概念掌握矩阵的初等变换并利用矩阵的初等变换简化行列式的计算。
第六节 行列式按一行(列)展开
1.理解余子式和代数余子式的概念;
2.掌握行列式按一行(列)展开计算行列式的方法;
3.掌握形如范德蒙德行列式的计算。
第七节 克拉默(Cramer)法则
2.理解并掌握克拉默法则。
第八节 拉普拉斯(Laplace)定理·行列式的乘法规则
1.掌握k阶子式的代数余子式的概念;
2.理解并掌握拉普拉斯定理和行列式的乘法原理。
第三章 线性方程组
第一节 消元法
1.掌握代入消元法和高斯消元法;
2. 理解方程组的初等变换。
第二节 n维向量空间
1.掌握n维向量的概念,掌握向量的加减法运算以及数与向量相乘。
第三节 线性相关性
1.理解线性相关,线性无关,线性表出,等价,极大线性无关组等概念。
2.掌握判断向量组线性相关和线性无关的方法,掌握将一个向量被其他向量线性表出的方法;
3.理解有关向量组线性相关性的若干结论。
第四节 矩阵的秩
1.掌握矩阵的行秩,列秩和秩的概念;
2.理解矩阵的秩与矩阵的子式的关系;
3.掌握计算矩阵的秩的方法,并求矩阵的列(行)向量组的极大线性无关组。
第五节 线性方程组有解的判定定理
1.理解并掌握线性方程组有解判定定理。
第六节 线性方程组界的结构定理
1.掌握齐次线性方程组的基础解系的概念;
2.理解并掌握(齐次)线性方程组的解的结构定理并能熟练求解线性方程组。
第七节 二元高次方程组
1.了解求解二元高次方程组的一般方法。
第四章 矩阵
第一节 矩阵概念的一些背景
1.了解矩阵概念的背景。
第二节矩阵的运算
1.掌握矩阵的四则运算以及矩阵的数量乘法并能熟练的应用各种运算性质进行计算。
第三节矩阵乘积的行列式与秩
1.理解矩阵乘积的行列式和行列式的乘积之间的关系;
2.掌握矩阵的各种运算的秩与原来矩阵的秩之间的关系。
第四节矩阵的逆
1.掌握可逆矩阵以及矩阵的伴随矩阵和矩阵的逆的概念;
2.掌握矩阵可逆的条件以及矩阵的逆的求法;
3.理解矩阵求逆与其他矩阵运算之间的关系并能求解简单的矩阵方程。
第五节 矩阵的分块
1.掌握矩阵分块原理,并利用矩阵分块原理解决相关问题。
第六节 初等矩阵
1.掌握初等矩阵的概念;
2.理解初等矩阵的乘法与矩阵的初等变换之间的关系,并利用初等矩阵解决相关问题。
第七节 分块乘法的初等变换及应用举例
1.掌握利用分块矩阵以及矩阵初等变换相结合简化矩阵运算的方法,并能利用来解题。
第五章 二次型
第一节 二次型及其矩阵表示
1.掌握二次型及其矩阵的定义,矩阵的合同关系;
2.理解二次型的线性替换和矩阵的合同关系之间的关系。
第二节 标准形
1.掌握利用二次型的非退化线性替换化二次型为标准形的方法及矩阵方法;
2.掌握利用上述方法化二次行为标准形的具体步骤并能用之解决问题。
第三节 唯一性
1.掌握实(复)二次型的规范型的概念;
2.理解规范型的唯一性定理及证明,并用之解决实际问题。
第四节 正定二次型
1.掌握正定二次型、负定二次型、半正定二次型、半负定二次型的概念;
2.理解正定二次型、负定二次型、半正定二次型、半负定二次型的所有等价条件并能灵活利用个等价条件解决问题。
第六章 线性空间
第一节 集合·映射
1.掌握集合与映射定义,理解单射,满射,可逆映射的定义,并能验证映射的可逆性并求映射的逆。
第二节 线性空间的定义与简单性质
1.掌握线性空间的定义会判断怎样的集合是线性空间;
2.掌握线性空间的简单性质,并利用性质解决相关问题。
第三节 维数·基与坐标
1.掌握维数、基、坐标的概念,会求线性空间的维数和基,对于任意一个向量会求他在某组基下的坐标;
第四节 基变换与坐标变换
1.理解线性空间任意两组基之间的关系,了解基变换矩阵,会通过基座标变换矩阵来求向量的坐标。
第五节 线性子空间
1.掌握线行子空间的概念和判定;
2.了解线行子空间的基和原线性空间的基之间的关系。
第六节 子空间的交与合
1.理解并掌握维数定理;
2.理解任意多个子空间的交仍是子空间,任意有限多个子空间的和是子空间。
第七节 子空间的直和
1.掌握子空间的直和的概念;
2.理解子空间的直和的判定条件,并会利用条件判断子空间的和是否位直和。
第八节 线性空间的同构
1.掌握线性空间同购的概念,会判断怎样的映射是同构映射;
2.理解并掌握线性空间的同构的充要条件并构造同构的线性空间之间的同构映射。
第七章 线性变换
第一节 线性变换的定义
1.掌握线性变换的概念及基本性质理解线性变换与映射的关系。
第二节 线性变化的运算
1.掌握线性变换的和、差、积、商,以及线性变换的数量乘积和逆仍然是线性变换。
第三节 线性变换的矩阵
1.掌握线性变换及其运算和矩阵及其运算之间的关系;
2.理解线性变换在不同基下的矩阵之间的相似关系,并了解相似关系的性质。
第四节 特征值与特征向量
1.掌握特征值、特征向量与特征多项式的概念;
2.理解特征值与特征向量之间的关系;
3.对于任意的线性变换(方阵)会求其特征多项式,特征值和特征向量。
4.理解相似的矩阵的特征多项式及特征值之间的关系。
第五节 对角矩阵
1.掌握任意方阵客对角化的所有充分必要条件,充分条件以及必要条件;
2.掌握判断矩阵可对角化的方法,并能将可对角化的矩阵对角化。
第六节 线性变换的值域与核
1.掌握线性变换的值域与核,秩与零度的概念;
2.理解线性变换的秩和零度的和等于线性空间的维数,并能用之解决问题。
第七节 不变子空间
1.掌握不变子空间的概念以及线性变换在子空间上的限制;
2.理解利用不变子空间简化线性变换(矩阵)的方法,并能利用它简化矩阵。
第八节 若尔当(Jordan)标准形
1.掌握矩阵的若尔当标准形的概念;
2.理解矩阵的若尔当块和其对应的线性空间的不变子空间的关系;
3.掌握将矩阵化为若尔当标准形的方法,并会利用该方法化矩阵为若尔当型矩阵。
第九节 最小多项式
1.掌握最小多项式的概念;
2.理解矩阵(线性变换)的最小多项式和特征多项式以及若尔当标准形的关系,并会求矩阵的最小多项式。
第八章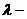 矩阵
矩阵
第一节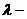 矩阵
矩阵
1.掌握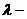 矩阵,
矩阵,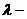 矩阵的秩的定义以及
矩阵的秩的定义以及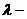 矩阵可逆的充要条件。
矩阵可逆的充要条件。
第二节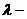 矩阵在初等变换下的标准形
矩阵在初等变换下的标准形
1.掌握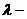 矩阵的初等变换,以及
矩阵的初等变换,以及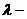 矩阵的标准形的定义;
矩阵的标准形的定义;
2.理解并掌握用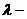 矩阵的初等变换化
矩阵的初等变换化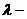 矩阵为标准形的方法,并能讲
矩阵为标准形的方法,并能讲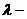 矩阵化为标准形。
矩阵化为标准形。
第三节 不变因子
1.掌握行列式因子和不变因子的定义,理解两者之间的关系,并会求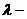 矩阵的不变因子和行列式因子;
矩阵的不变因子和行列式因子;
2.理解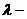 矩阵的标准形是唯一的。
矩阵的标准形是唯一的。
第四节 矩阵相似的条件
1.掌握理解用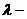 矩阵的等价和不变因子刻画矩阵相似,并能利用
矩阵的等价和不变因子刻画矩阵相似,并能利用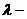 矩阵判断矩阵是否相似。
矩阵判断矩阵是否相似。
第五节 初等因子
1.理解行列式因子,不变因子,初等因子之间的关系;
2.掌握不变因子,初等因子的求法,并会求解不变因子和初等因子;
3.理解初等因子跟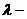 矩阵的标准形之间的关系。
矩阵的标准形之间的关系。
第六节 若尔当(Jordan)标准形的理论推导
1.掌握利用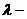 矩阵,不变因子,初等因子,解决矩阵的相似对角化问题以及矩阵的若尔当标准形问题。
矩阵,不变因子,初等因子,解决矩阵的相似对角化问题以及矩阵的若尔当标准形问题。
第七节 矩阵的有利标准形
1.掌握利用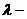 矩阵,解决矩阵的有理标准形问题的方法。
矩阵,解决矩阵的有理标准形问题的方法。
第九章 欧几里得空间
第一节 定义与基本性质
1.掌握内积的定义和性质;掌握欧几里得空间的定义;
2.掌握欧几里得空间中向量的长度和家教的概念,正交的概念;
3.掌握欧几里得空间的柯西-布涅科夫斯基不等式,以及度量矩阵。
第二节 标准正交基
1.掌握标准正交基的概念;
2.掌握施密特正交化方法,并学会利用施密特正交化方法求欧几里得空间的标准正交基;
3.掌握正交矩阵的概念,理解两组标准正交基之间的过渡矩阵是正交阵。
第三节 同构
1.理解欧几里得空间同构的概念。
第四节 正交变换
1.掌握正交变换的概念,理解正交变换在标准正交基下的矩阵是正交阵;
2.掌握正交变换的性质,并利用正交变换的性质解题。
第五节 子空间
1.掌握欧几里得空间的子空间的定义,掌握欧几里得空间的子空间的正交补的定义,并能够找出欧几里得空间的子空间的正交补。
第六节 实对称阵的标准形
1.理解掌握利用正交合同变换化实对称阵为对角阵的方法,并能解决相关问题。
第七节 向量到子空间的距离·最小二乘解
1.掌握距离的概念;
2.理解利用最小二乘法解决具体问题的方法。
第八节 酉空间介绍
1.掌握酉空间的定义和性质;
2.理解酉空间与欧几里得空间的共同点和差异。
第十章 双线性函数与辛空间
第一节 线性函数
1.掌握线性函数的概念。
第二节 对偶空间
1. 掌握对偶空间与对偶基的定义,并会求线性空间的对偶空间。
2. 掌握对偶空间的性质。
第三节 双线性函数
1.掌握双线性函数的概念,度量矩阵的概念;
2.了解双线性函数与矩阵的关系以及特别的双线性函数。
第四节 辛空间
1.掌握辛空间,辛同构,辛正交基,辛正交补等有关定义;
2.了解Witt定理。
(二)实践教学的内容及要求
无实践要求
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:多项式 |
25 |
21 |
|
|
4 |
|
|
|
第二章:行列式 |
25 |
21 |
|
|
4 |
|
|
|
第三章:线性方程组 |
25 |
19 |
|
|
6 |
|
|
|
第四章:矩阵 |
27 |
21 |
|
|
6 |
|
|
|
第五章:二次型 |
13 |
11 |
|
|
2 |
|
|
|
第六章:线性空间 |
15 |
11 |
|
|
4 |
|
|
|
第七章:线性变换 |
21 |
17 |
|
|
4 |
|
|
|
第八章: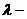 矩阵 矩阵 |
12 |
10 |
|
|
2 |
|
|
|
第九章:欧几里得空间 |
18 |
14 |
|
|
4 |
|
|
|
第九章:双线性函数与辛空间 |
6 |
6 |
|
|
|
|
|
|
合 计 |
187 |
151 |
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+期中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.北京大学数学系几何与代数教研室编 王萼芳、石生明修订《高等代数》(第三版),高等教育出版社,2003年。
(二)主要参考书目
1. 王萼芳,石生明修订《高等代数》,(第三版)高等教育出版社;
复旦大学数学系主编,《高等代数》,上海科技出版社1987年版;
解析几何教学大纲
教研室主任:王培合 执笔人:王培合
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:解析几何
课程编号:06200311
英文名称:Analytic Geometry
课程类型:专业基础课
总 学 时:68 理论学时:68 实验学时:0 课外学时:0
学 分:4
开设专业:信息与计算科学
先修课程:无
二、课程任务目标
(一)课程任务
《解析几何》作为大学数学的主要基础课程之一,是高等数学的主要组成部分。它对数学专业的学员后继课程的学习有重要而深刻的影响,它所提供的数学思想也是其它课程所无法替代的。
《解析几何》的基本思想是用代数的方法来研究几何。代数为几何提供研究方法,几何为代数提供直观背景。坐标法架起了几何与代数之间的桥梁。单纯的坐标是没有意义的,几何量的存在是要经得住合理的坐标变换的,因此选取好的坐标使几何量、几何关系的研究简单化是《解析几何》课程的主要任务之一。另外对空间关系的良好的理解力和想象力可以使复杂的数学结构变的直观简单,培养良好的空间想象能力也是本课程重要的教学目标之一。
(二)课程目标
在学完本课程之后,学生能够:
1.掌握三维欧氏空间的各种运算;
2.能够用坐标方法建立几何和代数之间的联系,能运用坐标向量等工具解决几何问题;
3.掌握点、线、面的方程形式以及它们之间的位置关系的方程描述,能解决有关点、线、面的实际问题;
4.对于空间中特殊的二次曲面的方程能够掌握方程和曲面之间的内在联系,能够用平行截割法研究曲面的形状,掌握常见的直纹面及其性质;
5.掌握二次曲线的化简和分类。
三、教学内容和要求
第一章 矢量与坐标
第一节 矢量的概念
1. 理解矢量的有关概念,掌握矢量间的关系;
2. 理解矢量的定义和两要素。
第二节 矢量的加法及其运算法则;
1. 理解矢量加法的定义及其运算法则;
2. 了解矢量加法的运算法则的证明过程;
3. 初步掌握矢量法证明问题的思想。
第三节 数量乘矢量及其运算法则
1. 理解矢量数乘运算的定义及其运算法则;
2. 掌握矢量加法的运算法则的证明过程;
3. 掌握利用矢量证明问题的思想及其解决问题的办法。
第四节 矢量的线性关系与矢量的分解
1. 掌握矢量之间的线性关系,理解共线、共面矢量的线性表示;掌握空间矢量的线性表示;
2. 理解线性相关的概念及其初步了解线性无关的概念;
3. 掌握线性相关和共线、共面的联系,掌握空间向量的结构;
第五节 标架与坐标
1. 理解标架的定义及其定比分点的定义;
2. 掌握点的坐标和矢量的坐标表示;
3. 理解坐标系的概念及其相关定义;
4. 掌握在坐标系之下矢量的各种运算的表示,能够用坐标法建立几何和代数之间的关系。
第六节 矢量在轴上的投射影
1. 了解轴的概念和点及其矢量在轴上射影的作图法,射影和射影矢量的关系,有向角的概念;
2. 掌握投影的计算及其运算性质。
第七节 两矢量的数性积
1. 了解数性积的物理背景;
2. 掌握数性积的定义及其运算性质;
3. 掌握数性积的坐标运算;
4. 了解平面向量的有向角表示。
第八节 两矢量的矢性积
1. 了解矢性积的物理背景及其几何意义;
2. 掌握矢性积的定义及其运算性质,理解矢性积运算的反交换律;
3. 掌握矢性积的坐标运算。
第九节 三矢量的混合积
1. 掌握矢量的混合积概念及几何意义;
2. 掌握混合积的运算性质及其坐标表示;
3. 掌握利用顶点坐标计算四面体的体积;
4. 掌握向量法及其坐标法解决问题的思想。
本章的重点是矢量的两个要素:模与方向;矢量加法的平行四边形法则、数量与矢量的乘法概念;矢量的三个分解定理及线性相关的判断;标架概念及其点和矢量的坐标表示方法;矢量在轴上的射影与射影矢量的概念;两矢量的数性积概念及几何意义;两矢量矢性积概念及几何意义;三矢量混合积概念及几何意义。
本章的难点包括运算律的证明、几何命题转化为矢量间的关系;分解定理的证明;射影与射影矢量的关系;根据数性积理论证明有关的命题;矢性积的几何意义;混合积的几何意义。
第二章 轨迹与方程
第一节 平面曲线的方程
1. 理解轨迹方程的概念和意义;
2. 了解平面曲线的轨迹方程的几种形式;
3. 掌握几种特殊曲线的方程。
第二节 曲面的方程
1. 理解曲面方程的定义;
2. 掌握曲面方程的几种形式。
第三节 母线平行于坐标轴的柱面方程
1. 了解母线平行于坐标轴的柱面方程的特点。
第四节 空间曲线的方程
1. 掌握空间曲线的方程;
2. 了解空间曲线的方程表示及其向量和坐标表示。
本章的重点是曲面和空间曲线的方程求法;母线平行于坐标轴的柱面方程的特征。
本章难点是根据给定图形的条件,选择适当坐标系建立图形的方程。
第三章 平面与空间直线
第一节 平面的方程
1. 理解平面论基本定理;
2. 掌握平面的各种方程(参数式、点位式、三点式、截距式、一般式、点法式及法式);
3. 掌握平面的各种方程之间的的互化。
第二节 平面与点的相关位置
1. 理解点和平面的位置关系的坐标表示;
2. 掌握点关于平面的离差及其计算,掌握点到平面的距离计算公式;
3. 了解平面对空间的划分。
第三节 两平面位置的位置关系
1. 理解并掌握两平面的位置关系的方程表示;
2. 了解两平面的夹角和距离。
第四节 空间直线的方程
1. 理解直线的方向角、方向余弦、方向数概念及求法;
2. 掌握直线的点向式方程(参数式、对称式、两点式)和一般方程;
3. 掌握直线的标准方程与一般方程转化方法。
第五节 直线与平面的相关位置
1. 理解直线与平面的位置关系及判别方法;
2. 掌握直线与平面的交角和距离的求法。
第六节 空间两直线的相关位置
1. 理解空间两直线的位置关系及判别方法;
2. 掌握空间两直线的交角和异面直线间的距离与公垂线方程的求法;
第七节 空间直线与点的相关位置
1. 理解点和直线的位置关系;
2. 掌握点到直线的距离计算。
第八节 平面束
1. 掌握有轴平面束和平行平面束的概念;
2. 掌握两种平面束的方程,掌握利用平面束计算问题的技巧;
3. 掌握直线一般方程之下共面的充要条件。
本章的重点包括平面的点位式、一般式和法式方程及其转化方法;点与平面的离差和两平面的位置关系;直线的标准方程与一般方程;直线与平面的位置关系;空间两直线的位置关系及判别方法;平面束的概念及平面束方程的求法。
本章的难点是平面各种方程之间的互化;点与平面的离差;标准方程与一般方程的转化方法;直线与平面的交角;异面直线间的距离与公垂线方程;空间直线与点的距离公式;空间直线与点的距离公式。
第四章 柱面、锥面、旋转曲面与二次曲面
第一节 柱面
1. 了解柱面的定义;
2. 掌握柱面的方程建立步骤。
第二节 锥面
1. 了解锥面的定义;
2. 掌握锥面的方程建立步骤;
3. 理解锥面的方程的特点。
第三节 旋转曲面
1. 了解旋转曲面的定义;
2. 掌握旋转曲面的方程建立步骤;
3. 掌握坐标平面上曲线绕坐标轴旋转得到的方程特点及其形状。
第四节 椭球面
1. 了解椭球面的标准方程;
2. 掌握讨论椭球面性质的方法及步骤;
3. 了解椭球面图形。
第五节 双曲面
1. 了解两种双曲面的标准方程;
2. 掌握讨论双曲面性质的方法及步骤;
3. 了解双曲面的图形。
第六节 抛物面
1. 了解椭圆抛物面和双曲抛物面的标准方程;
2. 掌握椭圆抛物面和双曲抛物面的性质;
3. 掌握椭圆抛物面和双曲抛物面的图形。
第七节 单叶双曲面与双曲抛物面的直母线
1. 理解直纹曲面的概念;
2. 掌握单叶双曲面和双曲抛物面的直母线方程求法;
3. 了解单叶双曲面和双曲抛物面的直母线性质。
本章的重点是柱面方程、锥面方程、旋转曲面方程的求法;椭球面的标准方程及性质;单叶双曲面和双叶双曲面的标准方程及性质;直纹曲面的概念。
本章的难点包括柱面、圆锥面的方程;单叶双曲面和双叶双曲面图形的画法;单叶双曲面和双曲抛物面的直母线方程求法。
第五章 二次曲线的一般理论
第一节 二次曲线和直线的位置关系
1. 掌握二次曲线的方程;
2. 理解二次曲线的各种记号及其不变量;
3. 掌握二次曲线和直线的位置关系,
第二节 二次曲线的渐近方向、中心、渐近线
1. 理解二次曲线的渐近方向、中心、渐近线的概念及其几何性质;
2. 掌握二次曲线的渐近方向、中心、渐近线的求法;
3. 掌握二次曲线的分类。
第三节 二次曲线的切线
1. 理解二次曲线的切线的定义及其分类;
2. 掌握二次曲线的切线的求法。
第四节 二次曲线的直径
1. 理解二次曲线的直径的定义;
2. 掌握二次曲线的直径的求法;
3. 掌握中心、线心和无心二次曲线的直径的特点;
4. 理解共轭方向和共轭直径及其求法。
第五节 二次曲线的主直径与主方向
1. 理解二次曲线的主直径的定义;
2. 掌握二次曲线的切线的求法;
3. 掌握二次曲线的特征方向和特征根的性质。
第六节 二次曲线的化简与分类
1. 掌握平面直角坐标系的坐标变换;
2. 掌握在平移和旋转之下二次曲线各自的不变量;
3. 掌握二次曲线的两种化简方法及其分类;
4. 理解一般二次曲线的作图。
第七节 应用不变量化简二次曲线的方程
1. 理解二次曲线的不变量和半不变量;
2. 掌握利用不变量化简和分类二次曲线。
本章的重点是二次曲线的渐近方向、中心、渐近线、切线、直径、主直径和主方向等基本概念和求法以及二次曲线的化简和分类。
本章的难点是二次曲线的化简和分类。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 矢量与坐标 |
16 |
14 |
|
|
2 |
|
|
|
第二章 轨迹与方程 |
4 |
3 |
|
|
1 |
|
|
|
第三章 平面与空间直线 |
18 |
14 |
|
|
4 |
|
|
|
第四章 柱面、锥面、旋转曲面和二次曲面 |
14 |
12 |
|
|
2 |
|
|
|
第五章 二次曲线的一般理论 |
16 |
12 |
|
|
4 |
|
|
|
合 计 |
68 |
55 |
|
|
13 |
|
|
|
五、考核说明
本课程采用闭卷考试,成绩评定采用百分制,计算方法为期末总评成绩=期末考试成绩*70%+期中考试成绩*20%+平时成绩,其中平时成绩采取10分制,包括课堂表现和作业成绩。期末总评成绩不低于60分为及格。
六、主要教材及教学参考书目
(一)主要教材
1. 吕林根等 《解析几何》 高等教育出版社 1987年
(二)主要参考书目
1. 陈志杰 《高等代数与解析几何》 高等教育出版社 2000年
2. 朱鼎勋等 《解析几何学》 北京师范大学出版社 1984年
3. 丘维声 《解析几何》 北京大学出版社 1996年
“离散数学”教学大纲
教研室主任: 郑召文 执笔人:杨淑娣
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:离散数学
课程编号:06200411
英文名称:Discrete Mathematics
课程类型:专业基础课
总 学 时: 51 理论学时:51 实验学时: 0 课外学时:0
学 分:3
开设专业:信息与计算数学
先修课程:高等代数(06200221)
二、课程任务目标
(一)课程任务
本课程是信息与计算数学专业的专业课程,是计算机科学中基础理论的核心课程。它以研究离散变量的结构和相互关系为主要目标,是一门新兴的工具性学科。课程主要分为数理逻辑、集合论、计数、数论及图论等5个部分。
本课程的任务是在68学时的时间内讲授命题逻辑、集合与关系、计数原理与技术、整数与整除、数论应用、图的基本概念以及几类重要的图等内容;使学生基本掌握离散数学中的一些基本概念及基本方法及它们的应用。
(二)课程目标
通过本课程的学习,使学生掌握《离散数学》的基本理论、基本方法和基本技巧,进一步培养和提高学生的抽象思维和逻辑推理能力,为学生今后学习一些后继课程(如数据结构、编译原理等)奠定必要的理论基础,也为学生从事计算机方面的工作研究,打下坚实的数学基础。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 命题逻辑
本章是数理逻辑的基础内容。简要介绍数理逻辑的发展和应用,通过讲授,使学生熟练掌握常用联结词、命题符号化、推理规则、判断推理有效的演绎法;掌握命题、真值表、对偶式、代入规则、替换规则、主析取(合取)范式,间接证法;了解联结词的扩充。
第三章 集合与关系
熟练掌握容斥原理、序偶、笛卡尔积、关系及其复合、关系的性质及判别方法、关系的闭包、集合的划分与覆盖、等价关系、等价类、相容关系、偏序关系、哈斯图的画法、极大元、极小元、上(下)界、上(下)确界、最大(小)元等概念;掌握集合的交、并、差、补、对称差的运算及其运算规律;掌握关系的交、并、逆、复合运算、闭包运算及其性质;掌握关系的矩阵表示和关系图;了解最大相容类、全序关系、良序关系。
第七章 计数原理与技术
熟练掌握基本计数原理、鸽洞原理、排列与组合公式、重集的排列与组合公式;了解递推关系及其解法。
第九章 整数与整除
熟练掌握素数、最大公因数、最小公倍数、带余除法、同余的定义及性质、威尔逊定理、欧拉函数、完全剩余系、简化剩余系、欧拉定理、费尔马小定理;掌握整数分解唯一性定理、完全(简化)剩余系的判别方法;了解孪生素数、歌德巴赫猜想。
第十一章 数论应用
熟练掌握一次同余式组及孙子定理;掌握一元一次同余式有解的充分必要条件、最基本的二次同余式、模p的二次(非)剩余,勒让德符号、高斯二次互反定理、RSA公钥密码系统;了解二次同余式的定义及解法、传统加密法。
第十六章 图的基本概念及其矩阵表示
熟练掌握图的定义、简单图、无向完全图、子图、生成子图、链(路)、圈(回路)、连通图、强连通图、最短链与关键路算法、图的邻接矩阵、Warshall算法求可达矩阵;掌握结点、边(弧)、有(无)向图、加权图、结点的度、握手定理、简单链(路)、基本链(路)、简单圈(回路)、基本圈(回路);了解混合图、零图、补图、关联矩阵。
第十七章 几类重要的图
熟练掌握欧拉圈(回路)、欧拉图的定义及充要条件、哈密顿圈(回路)、哈密顿图的定义及充分条件、必要条件、树的等价定义、生成树、最小生成树及其算法;掌握欧拉链(路)、哈密顿链(路)、有向图存在欧拉路(回路)的充要条件;了解图的闭包、森林、联结u和v的最短链及其G.Dantzig算法、有向树、二叉树、前缀码等。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:命题逻辑 |
9 |
8 |
|
|
1 |
|
|
|
第三章:集合与关系 |
9 |
8 |
|
|
1 |
|
|
|
第七章:计数原理与技术 |
5 |
4 |
|
|
1 |
|
|
|
第九章:整数与整除 |
8 |
6 |
|
|
2 |
|
|
|
第十一章:数论应用 |
8 |
6 |
|
|
2 |
|
|
|
第十六章:图论的基本概念及其矩阵表示 |
6 |
4 |
|
|
2 |
|
|
|
第十七章:几类重要的图 |
6 |
4 |
|
|
2 |
|
|
|
合 计 |
51 |
40 |
|
|
11 |
|
|
|
五、考核说明
本课程考核方式为考试。主要考核学生对基础理论,基本概念的掌握程度,以及学生实际应用能力。平时作业成绩占10%,期中考试成绩占20%,期末考试成绩占70%。
六、主要教材及教学参考书目
(一)主要教材
1.李盘林、李丽双、赵铭伟等,《离散数学》(第二版),高等教育出版社,2006年。
(二)主要参考书目
1.耿素云等,《离散数学教程》,北京大学出版社,2003年;
2.徐洁磐,《离散数学导论》(第二版),高等教育出版社,1991;
“数据结构”教学大纲
教研室主任: 赵京东 执笔人:叶传秀
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数据结构
课程编号:06200511
英文名称:Data Structure
课程类型:专业基础课
总 学 时:119 理论学时:85 实验学时:34 课外学时:0
学 分:6
开设专业:信息与计算科学专业
先修课程:C语言程序设计(17000210);离散数学(06200410)
二、课程任务目标
(一)课程任务
《数据结构》课程是讨论各种数据组织中的数据逻辑结构、存储结构以及有关操作算法的学科,是计算机类专业的一门专业基础课。其主要任务是使学生深入了解计算机加工的数据结构的特性,正确选用数据的逻辑结构、存储结构及相应的算法,掌握算法的时间分析和空间分析技术,达到较高的数据抽象能力和设计、分析程序的能力。实验课是本课程重要的教学环节,其目的是使学生更好地巩固和掌握所学内容,提高学生的编程能力。
(二)课程目标
在学完本课程之后,学生能够:
1. 深入了解计算机加工的数据结构的特性;
2. 正确选用数据的逻辑结构、存储结构及相应的算法;
3. 掌握算法的时间复杂性分析和空间复杂性分析方法;
4. 达到较高的数据抽象能力和设计、分析程序的能力。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 概论
第一节 绪论
1.了解数据结构的学科特点和所要研究的主要问题;
第二节 基本概念和术语
1.了解数据、数据元素、数据项、数据类型等基本概念及其相互间的关系;
2.了解数据结构的含义与常见的基本结构;
3.掌握ADT抽象数据类型的概念与定义
第三节 抽象数据类型的表示与实现
了解类C语言描述的特点和方法;
了解三元组的ADT描述;
第四节 算法和算法分析
掌握算法的特性;
掌握算法设计的目标;
了解算法效率度量的方法;
了解时(空)间复杂度的概念;
掌握语句频度和时(空)间复杂性的分析方法;
本章教学重点:
1.数据、数据元素、数据项;
2.逻辑结构和数据结构在概念上的联系与区别;
3.抽象数据类型和数据抽象;
4.评价算法优劣的标准及方法。
本章教学难点:
1.区别算法与程序;
2.逻辑结构、存储结构的联系与区别;
3.抽象数据类型与数据抽象;
4.算法的时间复杂度分析。
第二章 线性表
第一节 线性表的类型定义
1.了解线性表的结构特点;
2.了解线性表的ADT定义;
3.掌握常用线性表的合并及提纯算法;
第二节 线性表的顺序表示和实现
1.理解顺序表的存储特点;
2.掌握顺序表的定义及其基本操作(查询、插入、删除、合并等)的实现算法;
3.理解顺序表的时空复杂性分析的方法;
第三节 线性表的链式表示和实现
1.了解链式存储的特点;
2.掌握单链表的类型定义及其基本操作(查询、插入、删除、合并、逆置等)的实现算法;
3.理解静态链表的定义及相关算法;
4.掌握单循环链表的表示方法及其基本操作(查询、插入、删除等)的实现算法;
5.掌握双向链表的定义及其基本操作(查询、插入、删除等)的实现算法;
6.理解线性表的时空复杂性分析的方法;
第四节 一元多项式的表示及相加
1.了解一元多项式的表示方法;
2.理解一元多项式的ADT类型定义;
3.掌握一元多项式的加法、求导算法;
本章教学重点:
1.线性表的定义及逻辑上的特点;
2.顺序表上插入、删除和定位运算的实现;
3.单链表的结构特点及类型说明;
4.头指针和头结点的作用及区别;
5.指针操作;
6.定位、删除、插入运算在单链表上的实现;
7.循环链表、双链表的结构特点及其基本操作的实现。
本章教学难点:
1.线性表与线性结构的联系与区别;
2.头结点在链表中的作用;
3.指针操作;
4.删除、插入运算中的指针操作顺序;
5.双链表上指针的操作顺序;
6.一元多项式加法的实现。
第三章 栈与队列
第一节 栈
1.了解栈的定义和特点;
2.理解栈与一般的线性表的区别及其应用领域;
3.掌握顺序栈的定义和(初始化、取栈顶元表、入栈、出栈等)的实现算法;
4.掌握链栈的定义和基本操作(初始化、取栈顶元表、入栈、出栈等)的实现算法;
第二节 栈的应用举例
1.掌握数制转换的思想及其算法实现;
2.掌握括号匹配的思想及其算法实现;
3.理解行编辑程序的思想及其算法实现;
4.理解迷宫问题的求解思想及其算法实现;
5.掌握表达式求值的思想及其算法实现;
6.掌握前辍表达式、中辍表达式、后辍表达式的特点及其相互转换方法;
7.掌握后辍表达式求值的思想及其算法实现;
8.理解前辍表达式与后辍表达式的转换算法;
第三节 栈与递归的实现
1.了解递归的定义及其思想;
2.理解栈在递归算法中的作用;
3.掌握利用递归解决实际问题的方法;
第四节 队列
1.了解队列的定义和特点;
2.理解栈、队列与一般线性表的区别;
3.了解双端队列的特点和应用;
4.掌握链队列的定义及其基本操作(初使化、入队、出队等)的算法实现;
5.掌握循环队列的定义及其基本操作(初使化、入队、出队等的算法实现;
6.掌握循环队列中队满、队空的判别方法
本章教学重点:
1.栈的定义及逻辑特点;
2.栈上的基本运算;
3.栈的顺序存储结构及运算实现;
4.栈的链式存储结构;
5.入栈、出栈等运算在链栈上的实现;
6.栈在实际中的应用;
7.队列的定义及逻辑特点;
8.队列上的基本运算;
9.队列的顺序存储结构及其上的运算实现;
10.队列的链式存储结构;
11.入队、出队等运算在链队列上的实现。
本章教学难点
1.顺序栈的溢出判断条件;
2.栈的非递归算法;
3.栈在实际中的应用;
4.表达式的表示方法及其相互转换;
3.循环队列的队空、队满判断条件;
4.循环队列上的插入、删除操作。
第四章 串
第一节 串类型的定义
1.了解串类型的定义和特点;
2.了解空串和空格串的区别;
3.理解串相等的概念;
4.理解串的ADT类型定义;
5.掌握利用基本操作实现特定算法的方法;
第二节 串的表示和实现
1.了解三种存储结构的定义和存储特点;
2.掌握串的定长顺序存储表示和基本操作(联接、求子串等)的实现算法;
3.掌握串的堆顺序存储表示和基本操作(联接、求子串等)的实现算法;
4.理解串的块链存储的定义和基本操作(联接、求子串等)的实现算法;
5.掌握存储密度的定义及其求解方法;
第三节 串的模式匹配算法
1.理解模式匹配的定义;
1.掌握朴素的匹配算法的思想及其算法实现;
2.了解首尾匹配算法的思想及其算法实现;
3.掌握next数组和nextval数组的求解方法;
4.理解get_next和get_nextval算法的思想和求解过程;
5.掌握Kmp匹配算法的思想及其算法实现;
本章教学重点:
1.串的基本运算;
2.串的三种存储及其算法实现;
3.串的三种模式匹配算法;
4.Next数组和Nextval数组的求解;
5.块链存储的存储密度。
本章教学难点:
1.串的块链存储的定义及其基本操作的算法实现;
2.串的模式匹配算法的思想及其实现;
3. Next数组和Nextval数组的求解。
第五章 数组和广义表
第一节 数组的定义
1.了解数组的定义和特点;
2.了解数组和一般线性表的区别;
第二节 数组的顺序表示和实现
1.理解数组的按行存储和按列存储的特点;
2.掌握按行存储和按列存储的地址计算方法;
3.理解数组的顺序存储表示和基本操作的实现算法;
第三节 矩阵的压缩存储
1.了解特殊矩阵的特点;
2.理解稀疏阵的定义和稀疏因子;
3.掌握特殊阵(对称阵、对角阵、上(下)三角阵等)的存储特点和地址映射关系;
4.掌握稀疏阵的三元组顺序表的存储方式表示和矩阵的转置算法;
5.掌握稀疏阵的行逻辑链接的顺序表存储方式和矩阵乘法的算法实现;
6.掌握矩阵的十字链表的存储方式;
7.理解基于十字链表存储方式的矩阵算法的实现;
第四节 广义表的定义
1.了解广义表的定义和表现形式;
2.理解广义表的的特点和与一般线性表的区别;
3.掌握广义表的表头、表尾运算;
第五节 广义表的存储结构
1.掌握广义表的头尾链表存储表示;
2.掌握广义表的孩子、兄弟链表存储表示;
第六节 m元多项式的表示
1.理解m元多项式的表示算法;
第七节 广义表的递归算法
1.理解“分治”法的思想;
2.掌握广义表的深度算法的思想及其算法实现;
3.掌握广义表的复制算法的思想及其算法实现;
4.理解广义表的创建算法的思想及其算法实现;
本章教学重点:
1.数组的两种顺序存储方式;
2.数组元素的地址计算;
3.特殊阵(对称阵、对角阵、上(下)三角阵等)的存储特点和地址映射关系;
4.稀疏矩阵的三元组表存储及其矩阵的转置算法的实现。
5.稀疏矩阵的行逻辑链接存储及其矩阵的乘法算法的实现。
6.广义表的两种存储结构;
7.广义表的深度、复制算法的思想及其实现。
本章教学难点:
1.数组元素的地址计算;
2. 特殊阵(对称阵、对角阵、上(下)三角阵等)的存储特点和地址映射关系;
3. 矩阵的快速转置算法的实现;
4. 矩阵的乘法算法的实现。
5. 广义表的深度、复制、创建等算法的思想及其实现。
第六章 树和二叉树
第一节 树的定义和基本术语
1.了解树形结构的特点和与线性结构的区别;
2.了解抽象数据类型树的定义;
3.理解树结构中的一些基本术语;
4.了解抽象数据类型森林的定义;
第二节 二叉树
1.了解二叉树的定义和结构特点;
2.掌握二叉树的5种基本形态;
3.掌握二叉树的性质;
4.掌握二叉树的存储结构;
第三节 遍历二叉树和线索二叉树
1.理解二叉树遍历(先序、中序、后序、层次)的思想;
2.掌握二叉树遍历(先序、中序、后序、层次)的递归算法;
3.掌握二叉树遍历(先序、中序、后序、层次)的非递归算法;
4.掌握二叉树遍历(先序、中序、后序、层次)算法的应用;
5.了解线索二叉树的特点;
6.掌握二叉树的线索化(先序、中序、后序)思想和算法实现;
7.掌握线索二叉树中求(先序、中序、后)后继(前驱)的思想和算法实现;
第四节 树和森林
1.掌握树的三存储结构;
2.掌握森林与二叉树的相互转换方法;
3.理解树与森林的遍历方法;
4.理解树与森林、二叉树遍历的关系;
第六节 赫夫曼树及其应用
1.掌握路径长度、带权路径长度的概念;
2.理解最优二叉树的定义;
3.掌握构造赫夫曼树的思想和方法;
4.掌握赫夫曼编码的方法;
5.理解赫夫曼树及其赫夫曼编码的实现算法;
本章教学重点:
1.二叉树的性质;
2.二叉树的存储结构;
3.二叉树遍历(先序、中序、后序、层次)的递归算法;
4.二叉树遍历(先序、中序、后序、层次)的非递归算法;
5.二叉树遍历(先序、中序、后序、层次)算法的应用;
6.二叉树的线索化思想和算法实现;
7.线索二叉树中求(先序、中序、后)后继(前驱)的思想和算法实现;
8.树的三种存储结构;
9.森林与二叉树的相互转换;
10.构造赫夫曼树的思想和方法。
本章教学难点:
1.二叉树遍历的非递归算法;
2.二叉树遍历算法的应用;
3.二叉树的线索化;
4.线索二叉树中寻求后继、前驱的算法实现;
5.赫夫曼编码的算法实现。
第七章 图
第一节 图的定义和术语
1.了解图型结构的特点和与一般线性结构、树形结构的区别;
2.熟练理解图中的基本概念和相关术语;
第二节 图的存储结构
1.掌握图的邻接矩阵表示法及其相关基本操作的算法实现;
2.掌握图的邻接表表示法及其相关基本操作的算法实现;
3.理解图的十字链表表示法;
4.理解图的多重链表表示法;
第三节 图的遍历
1.掌握图的深度优先遍历的思想及其算法实现;
2.掌握图的深度优先遍历算法的应用;
3.掌握图的广度优先遍历算法的思想及其实现;
4.掌握图的广度优先遍历算法的应用;
第四节 图的连通性问题
1.掌握连通分量、强连通分量、生成树、最小生成树的概念;
2.理解连通分量、强连通分量的求解方法;
3.掌握普里姆算法求最小生成树的方法和思想;
4. 掌握克里斯卡尔算法求最小生成树的方法和思想;
5.理解最小生成树的生成算法;
6.掌握关节点的判别方法;
7.理解关节点的求解算法;
第五节 有身无环图及其应用
1.了解DAG的含义;
2.掌握拓扑排序的思想及其算法实现;
3.理解关键路径及其相关概念;
4.掌握关键路径的思想及其实现过程;
5.理解关键路径的求解算法;
第六节 最短路径
1.了解最短路径的相关概念;
2.掌握迪杰斯特拉求最短路径的思想;
3.理解迪杰斯特拉求最短路径的算法;
4.掌握弗洛伊德求最短路径的思想;
5.理解弗洛伊德求最短路径的算法;
本章教学重点:
1.图的邻接矩阵表示法及其相关基本操作的算法实现;
2.图的邻接表表示法及其相关基本操作的算法实现;
3.图的深(广)度优先遍历的思想及其算法实现;
4.图的深(广)度优先遍历算法的应用;
5.普里姆算法求最小生成树的方法和思想;
6.克里斯卡尔算法求最小生成树的方法和思想;
7.关节点的判别方法;
8.拓扑排序的思想及其算法实现;
9.关键路径的思想及其实现过程;
10.迪杰斯特拉求最短路径的思想;
11.弗洛伊德求最短路径的思想。
本章教学难点:
1.图的遍历算法;
2.关结点的求解算法;
3.最小生成树的实现算法;
4.拓扑排序的实现;
5.最短路径的算法实现。
第九章 查找
第一节 静态查找表
1.了解静态查找表的定义;
2.掌握顺序表的特点和定义;
3.掌握顺序表的查找算法;
4.掌握折半查找的思想及其算法实现;
5.掌握次优查找树的构造方法;
6.掌握分块查找的思想;
7.掌握各种查找表的性能分析方法;
第二节 动态查找表
1.了解动态查找表的特点和定义;
2.掌握二叉排序树的定义、性质、构造方法和基本操作的算法实现;
3.掌握平衡二叉树的定义、性质、构造方法和基本操作的算法实现;
4.掌握B-树的定义、性质、构造方法和基本操作的算法实现;
5.理解B+树和键树的定义;
6.掌握各种查找树的性能分析方法;
第三节 哈希表
1.理解哈希表的定义及其相关概念;
2.理解哈希函数的构造方法;
3.掌握处理冲突的方法;
4.掌握哈希表的查找性能分析方法;
5.理解哈希表的查找算法;
本章教学重点:
1.顺序表的查找算法;
2.折半查找的思想及其算法实现;
3.次优查找树的构造方法;
4.分块查找的思想;
5.各种静态查找表的性能分析方法;
6.二叉排序树的性质、构造方法和基本操作的算法实现;
7.平衡二叉树的定义、性质、构造方法和基本操作的算法实现;
8.B-树的定义、性质、构造方法和基本操作的算法实现;
9.处理冲突的方法;
10.哈希表的查找性能分析方法。
本章教学难点:
1.次优查找树的构造及其调整;
2.平衡二叉树的构造和基本操作的算法实现;
3.B-树的构造方法和基本操作的算法实现;
4.哈希表的查找性能分析方法;
5.哈希函数的选取。
第十章 内部排序
第一节 概述
1.了解排序的定义和相关概念;
2.理解排序的分类方法;
3.掌握排序算法性能分析的三个因素:比较、移动、稳定性;
第二节 插入排序
1.理解插入类排序的思想;
2.掌握直接插入排序、二路插入排序、希尔排序的过程和算法;
3.理解表插入排序的过程和算法;
第三节 快速排序
1.理解交换类排序的思想;
2.掌握冒泡排序及其改进的冒泡排序的思想和算法;
3.掌握快速排序的思想和算法;
第四节 选择排序
1.理解选择类排序的思想;
2.掌握简单选择排序的思想和算法;
3.理解树形选择排序的思想;
4.理解堆的定义和特点;
5.掌握堆选择排序的思想和建堆、利用堆排序的算法;
第五节 归并排序
1.理解归并类排序的思想;
2.掌握二路归并排序的思想和算法;
第六节 基数排序
1.了解基数排序的思想和特点;
2.了解LSD和MSD排序的方法;
3.掌握链式基数排序的方法;
4.理解链式基数排序的实现算法;
第七节 各种内部排序方法的比较讨论
1.掌握排序过程中时间性能的分析方法;
2.掌握排序过程中空间性能的分析方法;
3.掌握排序过程中算法稳定性的判定方法;
4.了解各种排序算法的比较方法;
本章教学重点:
1.各种内部排序的思想;
2.各种内部排序算法的性能(时间、空间、稳定性)分析方法;
3. 直接插入排序、希尔排序、快速排序、堆选择排序、二路归并排序的过程及其实现算法。
本章教学难点:
1.快速排序的过程及其算法实现;
2.堆的创建过程和算法以及利用堆进行选择排序的过程和实现算法;
3.链式基数排序的过程及其实现算法;
4.各种排序算法的性能分析。
第十一章 外部排序
第一节 外部信息的存取
1.了解信息的存取方式;
2.理解磁带信息存储的原理;
3.理解磁盘信息存储的原理;
第二节 外部排序的方法
1.掌握外部排序的方法;
2.掌握外部排序的时间计算方法;
第三节 多路平衡归并的实现
1.理解败者树的概念;
2.理解败者树的创建算法;
3.掌握败者树的构造方法;
第四节 置换-选择排序
1.理解置换—选择排序的思想;
2.掌握利用置换-选择排序思想进行产生初使归并段的方法;
3.掌握利用败者树进行多路归并的方法;
第五节 最佳归并树
1.理解最佳归并树的思想;
2.掌握最佳归并树的构造方法;
本章教学重点:
1.败者树的构造方法;
2.利用置换-选择排序思想进行产生初使归并段的方法;
3.利用败者树进行多路归并的方法;
4.最佳归并树的构造方法。
本章教学难点:
1.败者树的创建;
2.置换选择排序的方法;
3.利用败者树多路归并;
4.最佳归并树的构造。
(二)实践教学的内容及要求
实验1. 顺序表和单链表上的算法
了解C语言的编程环境及调式过程,理解顺序表和单链表的存储结构,掌握线性表的基本操作在两种存储结构上的实现算法。
实验 2.栈与队列
了解栈与队列的特点,理解栈与队列的存储类型,掌握入栈、出栈、入队、出队等基本操作的实现算法。
实验3.串
了解串的特点,理解串的定长顺序存储结构、堆顺序存储结构、块链存储结构,掌握串的基本操作的实现算法。
实验4.树与二叉树
了解树型结构的特点,理解树的二叉链表存储,掌握树的遍历算法。
实验5.图
了解图型结构的特点,理解图的邻接矩阵存储和图的邻接表存储,掌握图的遍历算法。
实验6.排序
了解排序的含义,理解各种内部排序的思想,掌握直接插入排序、选择排序、冒泡排序、快速排序、堆选择排序、二路归并排序的实现算法。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:绪论 |
4 |
4 |
|
|
|
|
|
|
第二章:线性表 |
12 |
8 |
4 |
|
|
|
|
|
第三章:栈与队列 |
12 |
8 |
4 |
|
|
|
|
|
第四章:串 |
6 |
6 |
|
|
|
|
|
|
第五章:数组和广义表 |
10 |
8 |
2 |
|
|
|
|
|
第六章:树与二叉树 |
18 |
12 |
6 |
|
|
|
|
|
第七章:图 |
18 |
12 |
6 |
|
|
|
|
|
第九章:查找 |
16 |
10 |
6 |
|
|
|
|
|
第十章:内部排序 |
16 |
10 |
6 |
|
|
|
|
|
第十一章:外部排序 |
7 |
7 |
|
|
|
|
|
|
合 计 |
119 |
85 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方式:闭卷;
总评成绩=期中成绩×0.2+平时(包括作业、上机实验考核,总分为10分)+期末成绩×0.7。
六、主要教材及教学参考书目
(一)主要教材
1.严蔚敏著《数据结构》(C语言版),清华大学出版社,1996年。
(二)主要参考书目
1.Adam Drozdek著《数据结构与算法――C++版》,清华大学出版社,2003年。
2.李平著《数据结构》(C语言版),电子工业出版社,2000年。
《常微分方程》教学大纲
教研室主任: 郑召文 执笔人:郑召文
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:常微分方程
课程编号:06200611
英文名称:Ordinary Differential Equations
课程类型:专业基础课
总 学 时: 51 理论学时:51 实验学时: 0 课外学时:4
学 分:3
开设专业:信息与计算数学
先修课程:无
二、课程任务目标
(一)课程任务
本课程系统讲授常微分方程的基本理论及基本解法,使学生掌握求解一些特殊类型方程的基本方法,掌握常微分方程的一些基本理论,以及培养学生运用常微分方程知识解决一些实际问题的能力。
(二)课程目标
在学完本课程之后,学生能够:
1.掌握微分方程与解的概念;
2.掌握微分方程的初等解法;
3.掌握存在惟一性定理、延展定理;
4.掌握高阶线性微分方程解的结构及常系数线性微分方程的解法;
5.掌握线性方程组的解的结构及常系数线性方程组的解法;
6.了解稳定性以及冲动奇点的分类.
三、教学内容和要求
(一)理论教学的内容及要求
第一章 初等积分法
第一节 掌握微分方程与解的概念
第二节 掌握变量可分离方程的解法
第三节 掌握齐次方程的解法
第四节 掌握一阶线性方程的解法
第五节 掌握全微分方程及积分因子的解法
第六节 了解线素场与欧拉折线
第七节 掌握一阶隐式微分方程的解法
第八节 了解一阶微分方程应用举例
第九节 了解几种可降阶的高阶方程的解法
第二章 基本定理
第一节 熟练掌握解的存在惟一性定理,证明解的存在惟一性
第二节 掌握解的延展定理,会判断解的存在区间
第三节 了解解对初值的连续依赖性
第四节 了解解对初值的可微性
第三章 线性微分方程
第一节 掌握线性方程的一般性质
第二节 熟练掌握线性齐次方程的基本理论
第三节 掌握线性非齐次方程的基本理论
第四节 掌握n阶常系数线性齐次方程解法
第五节 掌握 n阶常系数线性非齐次方程解法
第六节 会应用拉普拉斯变换求解初值问题的解。
第四章 线性微分方程组
第一节 掌握一阶微分方程组的一般理论
第二节 掌握线性微分方程组的基本概念
第三节 熟练掌握线性齐次方程组的基本理论
第四节 熟练掌握线性非齐次方程组的基本理论
第五节 掌握常系数线性微分方程组的解法。
第五章 定性与稳定性概念
第一节 了解相平面作图及单摆的运动方程
第二节 掌握初等奇点附近轨线的分布
第三节 会求所给系统的极限环
第四节 掌握稳定性的概念
(二)实践教学的内容及要求
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 初等积分法 |
12 |
10 |
|
|
2 |
|
|
|
第二章 基本定理 |
12 |
10 |
|
|
2 |
|
|
|
第三章 线性微分方程 |
10 |
8 |
|
|
2 |
|
|
|
第四章 线性微分方程组 |
10 |
8 |
|
|
2 |
|
|
|
第五章 定性与稳定性概念 |
7 |
7 |
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+期中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.东北大学数学系微分方程教研室编《常微分方程》,高等教育出版社,2003年(第二版)。
(二)主要参考书目
1.丁同仁 李成智《常微分方程教程》(第二版),高等教育出版社2004年版;
2.王高雄等《常微分方程》(第三版),高等教育出版社2006年版。
“概率论与统计学”教学大纲
教研室主任: 吕玉华 执笔人:温玉珍
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:概率论
课程编号:06200711
英文名称:Probability theory
课程类型:专业基础课
总 学 时: 51 理论学时:51 实验学时:0 课外学时:0
学 分: 3
开设专业:信息与计算数学专业
先修课程:数学分析(06200131)、高等代数(06200221)
二、课程任务目标
(一)课程任务
概率论基础是一入门课程,是继续学习数理统计、随机过程,以及与概率理论相关的课程的基础。它是从数量侧面研究随机现象规律的数学学科,理论严谨,应用广泛,发展迅速。概率论是一门应用性强的数学学科,广泛地应用于金融、保险,证券,工程技术和自然学科中,概率论与不同的问题结合形成许多分支。一方面,它有别开生面的研究课题,有自己独特的概念和方法,内容丰富,结果深刻;另一方面,它与其它数学分支又有紧密的联系,它是近代数学的重要组成部分。本课程知识是其他后继专业课程如数理统计,回归分析,随机过程,多元统计分析等的基础。 同时概率的基本知识现已成为中学数学课程的一部分,从而它也成为中学数学教师必须掌握的基础知识。
概率论课程的任务是使学生初步掌握处理随机现象的基本理论和方法,培养他们解决某些有关实际问题的能力。
在本课程的执行过程中,内容的选取和讲解都考虑到了学生以后的发展。
(二)课程目标
在学完本课程之后,学生能够:
1.对随机现象有充分的感性认识和比较准确的理解;
2.联系实际问题,初步掌握处理不确定性事件的理论和方法;
3.能够了解大量实际问题的类型及与概率论的联系,具备使用概率论知识来解决一些实际问题的能力。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 随机事件与概率
第一节 随机事件的直观意义及其运算
1.了解并理解必然现象、随机现象、随机试验、事件、事件的关系与运算、样本空间等概念;
第二节 概率的直观意义及其计算
1.了解古典概率的特点,理解古典概型中事件的概率;
2.掌握统计概率和几何概率的观念以及计算。
第三节 概率模型与公理化结构
1.理解概率的公理化定义;
第四节 条件概率
1.理解条件概率,掌握全概率公式、乘法公式和贝叶斯公式。
第五节 相互独立随机事件,独立试验模型
1. 理解事件的独立性。
2. 掌握串连和并联系统的可靠性计算。
3. 理解独立试验概型
第二章 随机变量及其分布函数
第一节 随机变量的直观意义与定义
1.了解离散型随机变量的定义,理解概率分布列及其基本性质;
2.了解连续型随机变量的定义,理解密度函数及其基本性质;
3.掌握分布函数及其基本性质
第二节 多维随机变量及其分布函数
1.了解二维随机变量的分布函数和边沿分布,并会计算有关事件的概率
第三节 相互独立随机变量,条件分布
1. 掌握相互独立随机变量与条件分布的意义和计算。
第四节 随机变量的函数及其分布函数
1.掌握和的分布、商的分布以及计算公式;
2.掌握随机变量的线性变换与平方变换
3. 掌握t-分布,F-分布和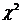 分布
分布
第三章 随机变量的数字特征
第一节 数学期望与方差
1.理解数学期望的定义;
2.掌握离散型随机变量与连续型随机变量的数学期望与方差
3.理解一般随机变量的数学期望与方差的定义;
第二节 矩
1.理解矩的定义和性质以及计算。
第三节 多维随机变量的数字特征
1.理解多维随机变量的数学期望与方差并掌握它们的计算;
第四节 多维随机变量函数的数字特征
1.理解多维随机变量函数的数学期望与方差并掌握它们的计算
第五节 条件数学期望
1.了解条件数学期望的定义和基本性质;
第四章 特征函数与极定理
第一节 一维特征函数的定义及其性质
1.掌握一维特征函数的定义及其性质
2.掌握特征函数与矩的联系
3掌握反演公式以及唯一性定理
第二节 多维随机变量的数字特征
1. 理解多维随机变量的数字特征的定义
2. 掌握二维随机变量的数字特征的性质
3. 掌握相互独立随机变量的和的特征函数的计算公式
第三节 母函数(*)
1.掌握母函数的定义及其性质。
第四节 大数定律
1.掌握弱大数定律
2. 了解强大数定律(*)
3. 了解依概率收敛与以概率为1收敛的关系(*)
第五节 中心极限定理
1. 掌握依分布收敛的概念
2. 掌握中心极限定理的几种不同形式并能加以应用
第六节 三种收敛的关系(*)
1.了解三种收敛的关系
第五章 测度与积分及其在概率论中的一些应用
第一节 为什么要引入测度与对测度的积分
1.了解相关背景知识
第二节 一般测度与勒贝格测度
1. 掌握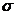 代数与测度的定义及其性质
代数与测度的定义及其性质
2. 掌握勒贝格外测度与测度的概念以及基本性质
3. 了解勒贝格可测集与Borel可测集的关系
第三节对测度的积分
1. 了解可测函数的概念;
2. 掌握可测函数对测度的积分以及积分的基本性质;
3. 掌握积分的极限性质;
4. 了解黎曼可积与勒贝格积分的关系
第四节在概率论中的应用
1. 了解可测变换、随机变量与概率分布的定义以及性质
2. 了解勒贝格-斯蒂尔切斯积分的定义
3. 了解积分变换定理与数学期望的关系
4. 掌握Radon-Nikodym定理
注:打(*)号内容可由教师选择是否讲授。
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:随机事件与概率 |
7 |
6 |
|
|
1 |
|
|
|
第二章:随机变量及其分布函数 |
11 |
9 |
|
|
2 |
|
|
|
第三章: 随机变量的数字特征 |
11 |
9 |
|
|
2 |
|
|
|
第四章:特征函数与极限定理 |
11 |
9 |
|
|
2 |
|
|
|
第五章:测度与积分及其在概率论中的一些应用 |
11 |
9 |
|
|
2 |
|
|
|
合 计 |
51 |
42 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
课程考试考核方法:闭卷考试:
总评=期末考试为主(70%)+期中考试(20%)+平时作业为辅(10%)
六、主要教材及教学参考书目
(一)主要教材
1.《概率论及数理统计》(上册) 梁之舜等编 高等教育出版社(2005年2月第三版)。
(二)主要参考书目
1.《概率论》,复旦大学编,人民教育出版社,1979年。
2.《概率论与数理统计教程》,魏宗舒等编,高等教育出版社,1983。
“普通物理”教学大纲
教研室主任:赵京东 执笔人:赵京东
一、课程基本信息
开课单位:物理科学学院
课程名称:普通物理
课程编号:06200811
英文名称:General Physics
课程类型:专业基础课
总 学 时:85 理论学时:65 实验学时:20 课外学时:0
学 分:5
开设专业:信息与计算数学
先修课程:数学分析(06200131)
二、课程任务目标
(一)课程任务
本课程是理工科非物理专业的一门必修的自然科学基础课。课程以学习经典物理学的基础知识为主,适当的介绍某些近代物理学内容,以力学、电学位重点,并力求结合数学专业的特点,充分利用所学的数学知识来组织教材和进行教学。通过本课程学习使学生掌握物理学基本概念、基本理论和基本规律,并运用物理学理论、观点和方法,分析、研究、计算或估计一些简单的物理问题,为学习数学理论提供必要的物理模型,了解物理学的研究方法,并为应用数学工具解决实际问题打下初步基础。
(二)课程目标
在学完本课程之后,学生能够:
1. 掌握物理学基本概念、基本理论和基本规律,并运用物理学理论、观点和方法,分析、研究、计算或估计一些简单的物理问题,为学习数学理论提供必要的物理模型;
2.了解物理学的研究方法,并为应用数学工具解决实际问题打下初步基础。
三、教学内容和要求
课程分为四部分:1.力学部分,2.热学部分,3.电磁学部分,4.光学和近代物理部分
(一)理论教学的内容及要求
课程教学重点:
非惯性系中的牛顿定律,动量与冲量,动量定理,动量守恒定律,机械能守恒定律、能量守恒定律,同方向同频率简谐振动的合成、复杂振动与简谐振动的关系,能量均分定理、理想气体内能,电流的功和功率、焦耳-楞次定律及微分形式,磁场线、磁通量、磁场高斯定理,毕奥-萨伐尔定律,电磁感应基本规律、法拉第电磁感应定律、楞次定律,次感应强度、磁场强度和磁化强度的关系,衍射现象、惠更斯-菲涅耳原理,单烽衍射、衍射光栅,爱因斯坦狭义相对论基本假设、洛仑兹变换,原子核的放射性衰变,核力、核模型等等
课程教学难点:
动量守恒定律,理想气体内能,电磁感应基本规律,法拉第电磁感应定律、楞次定律,爱因斯坦狭义相对论基本假设等等。
第一部分、力学部分
一、质点运动学
1.掌握参照系和坐标系、质点的概念
2.掌握位置矢量和运动方程、位移、速度和加速度的定义和计算
3.掌握路程和速率、自然坐标系中的速度和加速度
4.掌握直线运动、抛体运动、圆周运动
二、牛顿运动定律
1.掌握牛顿定律表述和意义
2.掌握牛顿定律应用举例
3.理解非惯性系中的牛顿定律
4.了解单位制和量纲简介
三、动量与冲量
1.掌握动量与冲量、动量定理
2.掌握动量守恒定律
3.理解碰撞的概念
四、功和能
1.掌握功和功率定义及计算
2.掌握动能和动能定理
3.掌握势能、功能原理
4.掌握机械能守恒定律、能量守恒定律
五、刚体的转动
1.掌握刚体的平动和定轴转动
2.掌握力矩、转动定律、转动惯量
3.掌握转动动能、力矩的功
4.掌握刚体的角动量、角动量守恒定律
六、机械振动和机械波
1.理解简谐振动特征
2.掌握简谐振动中的振幅、位相、周期和频率
3.掌握简谐振动的速度和加速度、简谐振动的能量
4.掌握同方向同频率简谐振动的合成、复杂振动与简谐振动的关系
5.掌握机械波的产生和传播、波长、频率和波速
6.掌握平面简谐波波函数、波的能量和波强
7.理解惠更斯原理、波的叠加原理、波的干涉衍射现象
第二部分、热学部分
一、气体分子运动轮
1. 掌握分子运动论的基本概念
2. 掌握气体状态参量、平衡态
3. 掌握理想气体状态方程
4. 理解压强、温度与微观量的联系
5. 掌握能量均分定理、理想气体内能
6. 掌握气体分子速率的统计分布规律、三种速率的意义与表达式
7. 理解分子的碰撞频率和平均自由程
二、热力学基础
1. 掌握系统的内能、功和热量
2. 掌握热力学第一定律
3. 掌握热力学第一定律对理想气体的应用,等容、等压、等温、绝热过程定量分析
4. 理解卡诺循环、热机效率、卡诺定理
5. 理解热力学第二定律
三、真实气体
1. 理解真实气体等温线、饱和蒸汽、临界状态
2. 掌握范德瓦尔斯方程
第三部分、电磁学部分
一、静电场
1. 掌握库仑定律
2. 掌握电场和电场强度
3. 掌握点电荷电场强度、场强叠加原理
4. 掌握电场线、电通量、真空和介质中的高斯定理
5. 掌握电场力的功、电势和电势差
6. 掌握点电荷的电势、电势叠加原理
7. 掌握场强与电势的微分关系
8. 掌握静电场中的导体、静电感应、静电屏蔽
9. 理解电场中的介质、电介质的极化
10. 掌握电容和电容器、电场的能量
二、直流电
1. 掌握稳恒电流、电流强度和电流密度
2. 掌握欧姆定律微分形式
3. 掌握电流的功和功率、焦耳-楞次定律及微分形式
4. 掌握电动势、闭合电路欧姆定律
5. 掌握基尔霍夫定律
三、电流的磁场
1. 掌握磁现象、磁场、磁感应强度
2. 掌握磁场线、磁通量、磁场高斯定理
3. 掌握毕奥-萨伐尔定律
4. 掌握安培环路定理、磁场强度、介质中安培环路定理
四、磁场对电流的作用
1. 掌握磁场对载流导线的作用力、安培定律
2. 掌握运动电荷受磁场作用力-洛仑兹力
3. 理解磁场对载流线圈的作用、磁矩
4、掌握平行电流间作用力-安培定义
五、电磁感应
1. 掌握电磁感应基本规律、法拉第电磁感应定律、楞次定律
2. 掌握动生电动势
3. 掌握感生电动势、涡旋电场
4. 掌握自感和互感、磁场的能量
六、物质的磁性
1. 掌握磁介质和磁化强度
2. 掌握次感应强度、磁场强度和磁化强度的关系
3. 理解铁磁质
七、电磁振荡和电磁波
1. 掌握麦克斯韦电磁方程组
2. 掌握电磁波的产生和传播
3. 理解电磁波谱
第四部分、光学和近代物理部分
一、光的干涉
1. 掌握光的单色性和相干性、相干光的获得
2. 理解双缝干涉、薄膜干涉、劈尖干涉
二.光的衍射
1. 掌握衍射现象、惠更斯-菲涅耳原理
2、掌握单烽衍射、衍射光栅
3. 了解光学仪器的分辨率
三、光的偏振
1. 掌握自然光和线偏振光、偏振片、马吕斯定律
2. 掌握反射和折射时光的偏振
3. 理解光的双折射现象
4. 了角旋光现象
四、狭义相对论基础
1、掌握伽利略变换和经典力学时空观
2. 了解爱因斯坦狭义相对论基本假设、洛仑兹变换
3. 了解相对论中的长度、时间和同时性
4. 了解相对论力学基础
五、光的量子性
1. 掌握绝对黑体辐射定律、光电效应
2. 了解普朗克量子假说、普朗克定律
3. 理解爱因斯坦方程、光子、光的波粒二象性
六、原子的量子理论
1. 掌握原子光谱、波尔的氢原子理论
2. 理解实物粒子的波粒二象性
3. 理解测不准关系
4. 掌握波函数、薛定谔方程
5. 了解一维势阱、氢原子的量子力学处理方法
6. 了解多电子原子系统、元素周期表
七、原子核和基本粒子简介
1. 了解核的组成和基本性质
2. 理解原子核的放射性衰变
3. 了解核力、核模型
4. 了解基本粒子简介
(二)实践教学的内容及要求
(安排必做实验12个,选做实验1个,设计实验1个。(关于实验项目、内容、要求及学时分配详见下表)
序号 |
实验项目名称 |
时数 |
必开/选开 |
目 的 要 求 |
实验类型 |
1 |
长度测量 |
3 |
必开 |
①掌握游标卡尺和螺旋测微器的使用及读数;②进一步掌握误差、有效数字的基本概念及运算法则。 |
综合型 |
2 |
固体密度的测定 |
3 |
必开 |
①进一步掌握游标卡尺的使用及读数;②掌握物理天平的正确使用方法及读数;③学会静力称衡法测量固体的密度。 |
综合型 |
3 |
弹簧倔强系数的测定 |
3 |
必开 |
①学会焦利氏秤的使用及读数规则;②掌握测弹簧倔强系数的原理;③学会用外推法求算弹簧的等效质量。 |
综合型 |
4 |
单摆测重力加速度 |
3 |
必开 |
①掌握用单摆法测重力加速度的原理;②学会停表的使用及读数;③学会用图解法处理数据。 |
验证型 |
5 |
自由落体运动研究 |
3 |
必开 |
①了解光电转换原理;②掌握自由落体加速度的测量原理;③学会用二次逐差法处理实验数据。 |
研究型 |
6 |
驻波法测定电振音叉频率 |
3 |
选开 |
①了解弦上形成的驻波波速的公式;②能利用驻波测出半波长;③能利用驻波法测定电振音叉的频率。 |
验证型 |
7 |
气垫导轨实验(一) |
3 |
选开 |
①了解气垫导轨的设计原理及使用方法;②验证牛顿第二定律。 |
设计型 |
8 |
气垫导轨实验(二) |
3 |
选开 |
①了解气垫导轨的设计原理及使用方法;②验证动量守恒定律。 |
设计型 |
9 |
用三线摆法测定刚体的转动惯量 |
3 |
选开 |
①理解用三线摆法测定刚体转动惯量的原理;②学会用三线摆法测匀质圆盘和圆环绕对称轴的转动惯量。 |
综合型 |
10 |
声速的测定 |
3 |
选开 |
①用驻波法测定空气中的声速(或用位相法测定空气中的声速);②学会用逐差法处理实验数据(利用李沙育图形的变化观测位相差);③测定声音的传播速度。 |
验证型 |
11 |
用拉脱法测液体的表面张力系数 |
3 |
必开 |
①了解液体的表面性质;②能用焦利氏秤测出液体的表面张力系数。 |
综合型 |
12 |
液体粘滞系数的测定 |
3 |
选开 |
①掌握用落球法测定液体的粘滞系数的原理;②熟练地运用基本仪器测量时间、长度和温度;③能测定液体的粘滞系数。 |
综合型 |
13 |
固体导热系数的测定 |
3 |
选开 |
①了解测导热系数的原理;②测定固体的导热系数。 |
综合型 |
14 |
电路接线练习与万用表使用 |
3 |
必开 |
①掌握滑线变阻器限流和分压的特点;②学会万用表的使用及读数规则。 |
综合型 |
15 |
用电流场模拟静电场 |
3 |
必开 |
①掌握用模拟法测绘静电场的原理和方法,从而加深对电场强度和电势概念的理解;②学习用模拟法测绘静电场的等势线和电场线;③学习用图示法表达实验结果。 |
验证型 |
16 |
用惠斯登电桥测量电阻 |
3 |
必开 |
①掌握惠斯登电桥测电阻的原理;②掌握用自组式惠斯登电桥测电阻的方法及箱式惠斯登电桥的使用方法;③了解提高电桥灵敏度的几种途径。 |
综合型 |
17 |
伏安法测晶体二极管的特性 |
3 |
必开 |
①能正确使用安培表和伏特表;②掌握测量伏安特性的两种方法及其修正;③了解二极管的伏安特性并作其特性曲线。 |
综合型 |
18 |
电表的扩程和校准 |
3 |
必开 |
①熟悉电流表、电压表的构造原理并了解电表改装的原理和方法;②学习扩程和校准电流表、电压表的基本方法;③了解校准曲线的意义。 |
综合型 |
19 |
用电位差计校准电表 |
3 |
选开 |
①了解补偿法原理;②初步掌握电位差计的使用;③学会用电位差计校准电表的方法;④了解电表的引用误差分布和电表的准确度级别的确定。 |
综合型 |
20 |
热敏电阻的特性研究 |
3 |
选开 |
①了解电阻的热敏特性;②研究电阻与温度的关系。 |
研究型 |
21 |
示波器的原理和使用 |
3 |
选开 |
①了解示波器的面板结构及各旋钮的功能;②理解简谐波的合成原理。 |
综合型 |
22 |
用电磁感应法测磁场分布 |
3 |
选开 |
①掌握用电磁感应法测磁场分布的原理;②描绘磁场分布 |
综合型 |
23 |
用牛顿环测平凸透镜的曲率半径 |
3 |
必开 |
①观察牛顿环产生的等厚干涉现象,加深对等厚干涉的认识;②掌握利用牛顿环测平凸透镜曲率半径的原理。 |
综合型 |
24 |
薄透镜焦距的测定 |
3 |
必开 |
①掌握测定凸透镜焦距的方法,加深对透镜成象公式的了解;②了解不同物距下凸透镜成象性质的规律;③掌握共轴光具的调节。 |
验证型 |
25 |
光栅常数的测定 |
3 |
选开 |
①加深对光栅衍射的理解;②初步掌握分光计的调节方法;③掌握用光栅测波长及由波长测光栅常数的方法。 |
综合型 |
26 |
单缝衍射的条纹位置及强度分布 |
3 |
选开 |
①测量夫琅和费单缝衍射的条纹位置和光强分布,加深对光的衍射现象的理解;②了解He—Ne激光的特点和应用;③掌握使用光点检流计测量光的相对强度的方法。学会测定透镜焦距的原理和方法。 |
综合型 |
27 |
液体折射率的测定 |
3 |
选开 |
①掌握测定液体折射率的原理和方法;②能正确测得液体的折射率。 |
验证型 |
24 |
用显微镜测量微小长度 |
3 |
选开 |
①了解测量微小长度的原理;②能正确读数。 |
综合型 |
25 |
光电效应 |
3 |
选开 |
①了解光电效应的基本规律,加深对光量子性的理解;②了解光电管的结构和性能,并测定其基本特性曲线;③验证爱因斯坦光电效应方程,测定普朗克常数。 |
综合型 |
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一部分:力学部分 |
21 |
16 |
5 |
|
|
|
|
任选一个设计型实验 |
第二部分:热学部分 |
17 |
12 |
5 |
|
|
|
|
第三部分:电磁学部分 |
30 |
25 |
5 |
|
|
|
|
第四部分:光学和近代物理部分 |
17 |
12 |
5 |
|
|
|
|
合 计 |
85 |
65 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+期中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.程守洙等《普通物理学》,高等教育出版社2001年第5版
(二)主要参考书目
1.汤毓骏《大学物理新编》,中国纺织大学出版社 2001年第2版。
2.张三慧《大学物理学》,清华大学出版社 2000年第2版
“数值代数”教学大纲
教研室主任:赵京东 执笔人:林秀丽
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数值代数
课程编号:06200911
英文名称:Numerical Algebra
课程类型:专业基础课
总 学 时:51 理论学时:51 实验学时:0 课外学时:0
学 分:3
开设专业:信息与计算科学专业
先修课程:高等代数(06200221)、数学分析(06200131)
二、课程任务目标
(一)课程任务
本课程是信息与计算科学专业基础课程。数值代数又称矩阵计算,数值代数研究的主要目的是如何针对各类科学与工程问题所提出的矩阵计算的特点,设计出相应的快速可靠的算法。
(二)课程目标
(1)掌握线性方程组的直接解法和迭代解法,最小二乘法,矩阵的特征值和特征向量的计算方法,掌握算法的设计思想和设计方法。学会分析数值计算中舍入误差对计算结果的影响,各种计算方法的收敛条件和收敛速度。
(2) 为今后从事科学计算,信息技术等专业的学生打下一个良好的知识基础。
三、教学内容和要求
第一章 绪论
教学重点和难点
绝对误差、相对误差、误差限和有效数字的定义及其相互关系,问题的条件分析和设计稳定
的数值算法要注意的问题,向量题范数和矩阵范数的定义及其性质,Givens变换,Householder变换
第一节 线性代数计算方法的重要性
1.了解研究数值代数的重要及必要性;
2.掌握数值代数的基本内容。
第二节 误差
1.了解误差来源以及以及舍入误差、截断误差的定义;
2.掌握绝对误差、相对误差、误差限和有效数字的定义和相互关系。
第三节 浮点运算和舍入误差
1.了解数的浮点表示及其之间的算术运算,常用的误差分析方法;
2.掌握向前、向后误差分析方法,会作简单的误差分析。
第四节 问题的条件和算法的数值稳定性
1.理解问题的条件和算法数值稳定性的概念;
2.掌握问题的条件分析和设计稳定的数值算法要注意的问题。
第五节 向量范数和矩阵范数
1.熟练掌握向量题范数和矩阵范数的定义及其性质;
2.理解向量序列和矩阵序列的收敛性,掌握矩阵的谱半径及其与范数之间的关系。
第六节 Givens变换和Householder变换
1.熟练掌握实数范围内的Givens变换和Householder变换及特点;
2.了解复数范围的两种变换。
第二章 解线性代数方程组的直接方法
教学重点和难点:Gauss消去法,列选主元Gauss消去法,三角分解法,追赶法,平方根法,最小二乘法。
第一节 Gauss消元法
1.理解Gauss消元法原理及实现条件,掌握Gauss消元法和列选主元消元法求解方程组的算法;;
2.了解全选主元消元法。
第二节 矩阵的三角分解
1.掌握用Doolittle及Crout分解法求方程组的解,能直接用矩阵乘法进行系数矩阵LU分解;
2.理解列主元三角分解法及三角分解法与Gauss消元法之间的关系。
第三节 带状对角形方程组的解法
1.理解带状对角形矩阵的概念,掌握求解三对角方程组的追赶法。
第四节 正定矩阵的Cholesky分解
1.了解正定矩阵的性质,掌握Cholesky分解(即平方根法)和改进的平方根法。
第五节 Gauss-Jordan消元法和矩阵求逆
1.掌握Gauss-Jordan消元法及其应用,如求解方程组集和矩阵的逆。
第六节 行列式计算
1.理解掌握利用Gauss消元和三角分解法求矩阵的行列式的方法。
第七节 计算解的精确度问题
掌握线性方程组的敏度分析和误差分析;
了解计算解误差的常用估计方法及解的迭代改善方法。
第八节 Gauss列主元消元法的舍入误差分析
1.了解Gauss列主元消元法的舍入误差分析。
第九节 线性最小二乘法
1.掌握数据拟合的最小二乘法及超定方程组与法方程之间的关系;
2.理解掌握矩阵QR分解的G-S与Householder方法,了解极小最小二乘解。
第三章 解线性代数方程组的迭代方法
教学重点与难点: Jacobi迭代,Gauss-Seidel迭代,超松驰迭代法,最速下降法,共轭梯度法。
第一节 迭代法的一般理论
1.掌握迭代法构造和迭代法收敛的充分必要条件,迭代法的误差分析;
2.了解迭代的可对称化和块迭代。
第二节 Jacobi迭代法
1.熟练掌握Jacobi迭代法的迭代格式、收敛性,并能判断收敛性;
2.了解块Jacobi迭代。
第三节 Gauss-Seidel迭代法
1.熟练掌握Gauss-Seidel迭代法的迭代格式、收敛性,并能判断收敛性;
2.了解块Gauss-Seidel迭代。
第四节 松弛迭代法
1.掌握松弛迭代法迭代法的迭代格式、收敛性;
2.了解最优松弛因子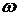 意义及块松弛迭代法和对称松弛迭代法。
意义及块松弛迭代法和对称松弛迭代法。
第五节 Chebyshev加速迭代法
1.理解多项式加速迭代法和Chebyshev加速迭代法。
第六节 共轭梯度法
1.理解掌握线性方程组和二次函数的极小值问题之间的关系,掌握最速下降法、共轭方向法、共轭梯度法基本思想;
2. 理解共轭梯度法的性质。
第四章 非对称矩阵特征值问题
教学重点和难点 幂法,反幂法,QR方法。
第一节 矩阵特征值的基本性质
1. 掌握矩阵特征值的圆盘第一、第二定理及其应用;矩阵特征值问题的总体条件数;
2.了解矩阵特征值问题的个体条件数。
第二节 幂法
1.熟练掌握幂法的基本算法及其主特征值为单根时的收敛性;
2.了解幂法的原点位移加速。
第三节 反幂法
1.掌握反幂法的基本算法及Rayleigh商迭代法;
2.了解带原点位移的反幂法及Rayleigh商迭代法的渐近收敛速度。
第四节 矩阵收缩
1.理解矩阵收缩的算法步骤。
第五节 QR方法
1. 掌握QR方法、Hessenberg矩阵的QR算法以及带原点位移的QR算法;
2. 了解实矩阵的双重步QR算法,QR算法的收敛性。
第六节 广义特征值问题
1.了解广义特征值问题的QZ算法。
第五章 对称矩阵特征值问题
教学重点和难点 幂法,对称QR方法,Jacobi方法,二分法及矩阵奇异值分解定理。
第一节 基本性质
1. 掌握实对称矩阵的谱分解定理和极值定理;
2.了解实对称矩阵特征值的估计和摄动。
第二节 幂法和子空间迭代法
1.掌握实对称矩阵的幂法和反幂法;
2.理解子空间迭代法。
第三节 对称QR方法
1.掌握矩阵的三对角化及其QR算法;
2.理解隐位移的QR算法。
第四节 矩阵收缩
1.理解矩阵收缩的算法步骤。
第五节 实对称矩阵的Jacobi方法
1.掌握实对称矩阵的Jacobi算法及其收敛性;
2.了解过关Jacobi方法。
第六节 奇异值分解算法
1.掌握矩阵奇异值及其分解定理;
2.理解双对角线矩阵的隐位移QR算法。
第七节 对称广义特征值问题
1.了解对称广义特征值问题。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:绪论 |
8 |
6 |
|
|
2 |
|
|
|
第二章:解线性代数方程组的直接方法 |
14 |
12 |
|
|
2 |
|
|
|
第三章:解线性代数方程组的迭代解法 |
13 |
11 |
|
|
2 |
|
|
|
第四章:非对称矩阵特征值问题 |
8 |
6 |
|
|
2 |
|
|
|
第五章:对称矩阵特征值问题 |
8 |
6 |
|
|
2 |
|
|
|
合 计 |
51 |
41 |
|
|
10 |
|
|
|
五、考核说明
考核方式:闭卷;
总评成绩=期中成绩×0.2+平时(包括作业、上机实验考核,总分为10分)+期末成绩×0.7。
六、主要教材及教学参考书目
(一)主要教材
1.蒋长锦,线性代数计算方法,中国科学技术大学出版社,2003年。
(二)主要参考书目
1.徐树方,数值线性代数,北京大学出版社,2002年。
2.曹志浩, 数值线性代数. 复旦大学出版社, 1996。
“信息论与编码理论”教学大纲
教研室主任: 赵京东 执笔人:杨淑娣
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:信息论与编码理论
课程编号:06201011
英文名称:Information and Coding Theory
课程类型:专业基础课
总 学 时:51 理论学时:51 实验学时: 0 课外学时:0
学 分:3
开设专业:信息与计算科学专业
先修课程:概率论(06200711)
二、课程任务目标
(一)课程任务
本课程是信息与计算数学专业的专业课程,是数学的一个重要的分支。课程主要分为香农信息论与代数编码理论两大部分。
本课程的任务是在68学时的时间内讲授信息量,信源编码理论,信道编码理论,代数码的基本内容,信息与编码的几个应用问题等内容;使学生基本掌握信息论与编码理论中的一些基本概念及基本方法。
(二)课程目标
本课程主要采用概率论、随机过程、近世代数等数学方法研究信息的测度、信道容量以及信源
和信道编码定理等理论问题,并研究具体的信息编码方法。其目的是掌握提高信息系统的可靠性和有效性的理论和方法,了解信息论与编码理论的全貌与应用背景。
三、教学内容和要求
理论教学的内容及要求
通过学习本课程能使学生掌握信息论与编码理论的基本概念,基本定理以及解决问题的基本方法,不但应该对信息论与编码理论的基本概念和基本定理及方法有比较系统的理解,而且应能掌握处理信息论与编码理论问题的一般方法。进而注意培养解决信息论问题所必需的理论能力达到为进一步学习和从事数学工作打下基础的目的。
概论
介绍信息论与编码理论的基本情况,信息度量的基本要求与通信系统的基本要素及它们的数学
模型。使学生了解信息论与编码理论的全貌。
信息量
重点讲授熵的定义及性质。围绕熵的定义介绍互信息及相关定义,简要介绍信息量的几个问题。
掌握熵、条件熵、互熵、条件熵的性质、互信息量、平均互信息量的概念及性质。
第三章 信源编码
阐明信源编码中的基本概念及编码规则。掌握离散信源编码的目的和模型,消息在编码信道上的信息传输速率,信源编码的编码效率,最佳编码,等长代码组的信源编码定理,不等长代码组的信源编码定理,仙农第一定理,最佳编码方法。
第四章 信道编码定理
主要阐明信道编码中的基本概念及编码规则。讲授几个重要的编码定理与逆编码定理,介绍信道容量的计算方法。掌握有扰离散信道的统计特性,消息在有扰离散信道上的信息传输速率,离散信道的信道容量,信道编码定理
第五章 抽象代数的基本知识
简单介绍抽象代数及域上的线性代数的部分基本知识。
第六章 编码理论的基本知识
介绍代数码的基本定义与纠错、检错能力,编码理论的基本问题。掌握码的最小汉明距离,码字的重量,码的最小重量及检、纠错能力的概念。
第七章 线性码
掌握线性码的定义,生成矩阵、校验矩阵的概念,线性码的对偶码,译码方法及重量分布。
第八章 汉明码
掌握汉明码的定义、性质及译码方法,了解极长码的定义。
第九章 循环码
掌握循环码的定义,码字多项式,循环码的生成多项式,生成矩阵,校验多项式和校验矩阵。掌握循环码的编码方法和译码方法。
第十章 BCH码和Reed-Solomon码
掌握BCH码和Reed-Solomon码的定义、基本性质、译码方法及重量分布。
第十一章 一些重要的线性码
了解Golay码、Reed-Mulller码、平方剩余码及Goppa码的定义。
第十二章 若干应用问题
了解有失真数据压缩问题、卷积码理论及其应用问题、汉字信息处理问题、条码技术等。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 概论 |
2 |
2 |
|
|
|
|
|
|
第二章 信息量 |
5 |
4 |
|
|
1 |
|
|
|
第三章 信源编码 |
5 |
4 |
|
|
1 |
|
|
|
第四章 信道编码定理 |
9 |
8 |
|
|
1 |
|
|
|
第五章 抽象代数的基本知识 |
7 |
6 |
|
|
1 |
|
|
|
第六章 编码理论的基本知识 |
2 |
2 |
|
|
|
|
|
|
第七章 线性码 |
5 |
4 |
|
|
1 |
|
|
|
第八章 汉明码 |
3 |
2 |
|
|
1 |
|
|
|
第九章 循环码 |
4 |
3 |
|
|
1 |
|
|
|
第十章 BCH码和Reed-Solomon码 |
4 |
3 |
|
|
1 |
|
|
|
第十一章 一些重要的线性码 |
3 |
2 |
|
|
1 |
|
|
|
第十二章 若干应用问题 |
2 |
2 |
|
|
|
|
|
|
合 计 |
51 |
42 |
|
|
9 |
|
|
|
五、考核说明
本课程考核方式为考试。主要考核学生对基础理论,基本概念的掌握程度,以及学生实际应用能力。平时作业成绩占10%,期中考试成绩占20%,期末考试成绩占70%。
六、主要教材及教学参考书目
(一)主要教材
1.沈世镒 陈鲁生, 信息论与编码理论, 科学出版社 2002年.
(二)主要参考书目
1.朱雪龙,应用信息论基础,清华大学出版社,2001年
2.万哲先,代数与编码,科学出版社,1985年
“数字信号处理”教学大纲
教研室主任:赵京东 执笔人:李本星
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数字信号处理
课程编号:06201111
英文名称:Digital Signal Processing
课程类型:专业基础课
总 学 时:34 理论学时:34 实验学时: 0 课外学时:0
学 分:2
开设专业:信息与计算科学专业
先修课程:概率论(06200711)
二、课程任务目标
(一)课程任务
本课程是信息与计算数学专业的专业课程,是数学的一个重要的分支,主要讲述数字信号处理的基本概念、原理及方法,其教学任务是在68学时的时间内讲授信号频谱和傅氏变换,离散信号和抽样原理,滤波与褶积、Z变换,线性时不变系统,冲击函数,希尔伯特变换,相关分析,离散物理可实现信号的性质和最小相位信号、最小能量延迟信号等内容。本课程将通过讲课、练习使学生掌握数字信号处理的基本理论和方法。
(二)课程目标
通过本课程的学习,应使学生掌握《数字信号处理》的基本理论、基本方法和基本技巧,培养学生利用计算机进行数字信号处理的基本思想方法和技巧,为以后从事数字信号处理的工作和进一步学习信息与计算数学专业课程打下基础。
三、教学内容和要求
理论教学的内容及要求
本课程是信息与计算数学专业的专业课程,主要讲述数字信号处理的基本概念、原理及方法,主要内容包括信号频谱和傅氏变换,离散信号和抽样原理,滤波与褶积、Z变换,线性时不变系统,冲击函数,希尔伯特变换,相关分析,离散物理可实现信号的性质和最小相位信号、最小能量延迟信号等。本课程将通过讲课、练习使学生掌握数字信号处理的基本理论和方法,为以后从事数字信号处理的工作和进一步学习信息与计算数学专业课程打下基础。
第一章 信号频谱和傅氏变换
介绍信号的连续、离散频谱,傅氏变换,频谱的基本性质。掌握傅氏变换,频谱的基本性质。
第二章 离散信号和抽样定理
重点讲授连续信号的离散化及由连续信号的离散化所引起的抽样问题。
第三章 滤波与褶积,Z变换
掌握连续、离散信号的滤波与褶积,能谱与能量等式,功率谱与平均功率等式,离散信号的Z变换。
第四章 线性时不变滤波器与系统
掌握线性时不变系统的概念、性质,系统的组合及时间响应函数。
第五章 冲激函数—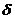 函数
函数
了解特殊的广义函数: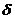 函数
函数
第六章 希尔伯特变换与实信号的复数表示
掌握希尔伯特变换定义,连续、离散实信号及物理可实现信号的希尔伯特变换。
第七章 有限离散傅氏变换
掌握有限离散傅氏变换、快速傅氏变换,了解快速傅氏变换的某些应用。
第八章 相关分析
掌握相关的定义、性质,循环相关与普通相关,了解利用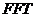 计算相关函数。
计算相关函数。
第九章 物理可实现信号、最小相位信号和最小能量延迟信号
掌握物理可实现信号、最小相位信号和最小能量延迟信号的概念与性质,这三类信号的Z变换
第十章 有限长脉冲响应滤波器和窗函数
了解几种时窗函数、最佳时窗函数,广义线性相位有限长脉冲响应滤波器的概念和设计方法。
第十一章 递归滤波器的设计
掌握递归滤波的概念及性质,了解几种模拟滤波器及数字递归滤波器的设计。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 信号频谱和傅氏变换 |
3 |
2 |
|
|
1 |
|
|
|
第二章 离散信号和抽样定理 |
3 |
2 |
|
|
1 |
|
|
|
第三章 滤波与褶积,Z变换 |
5 |
4 |
|
|
1 |
|
|
|
第四章 线性时不变滤波器与系统 |
3 |
2 |
|
|
1 |
|
|
|
第五章 冲激函数—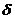 函数 函数 |
3 |
2 |
|
|
1 |
|
|
|
第六章 希尔伯特变换与实信号的复数表示 |
3 |
2 |
|
|
1 |
|
|
|
第七章 有限离散傅氏变换 |
7 |
6 |
|
|
1 |
|
|
|
第八章 相关分析 |
3 |
2 |
|
|
1 |
|
|
|
第九章 物理可实现信号、最小相位信号和最小能量延迟信号 |
8 |
7 |
|
|
1 |
|
|
|
第十章 有限长脉冲响应滤波器和窗函数 |
3 |
2 |
|
|
1 |
|
|
|
第十一章 递归滤波器的设计 |
3 |
2 |
|
|
1 |
|
|
|
合 计 |
34 |
33 |
|
|
11 |
|
|
|
五、考核说明
本课程考核方式为考试。主要考核学生对基础理论,基本概念的掌握程度,以及学生实际应用能力。平时作业成绩占10%,期中考试成绩占20%,期末考试成绩占70%。
六、主要教材及教学参考书目
(一)主要教材
1.程乾生,数字信号处理, 北京大学出版社, 2003年.
(二)主要参考书目
1.K.R.Rabiner and R.W.Schafer,Digital Processing,Prentice-Hall,Inc.,1996;
2.黄建国、刘树棠译,离散时间信号处理,科学出版社,1998。
“运筹与优化”教学大纲
教研室主任:郑召文 执笔人:苗翠霞
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:运筹与优化
课程编号:06201212
英文名称:Operations Research
课程类型:专业方向限选课
总 学 时:68 理论学时:64 习题课时:4 课外学时:
学 分:4
开设专业:信息与计算科学
先修课程:数学分析(06200131) 高等代数(06200221) 概率论(06200711)
二、课程任务目标
(一)课程任务
运筹学课程是数学与应用数学专业,信息与计算科学 统计学的必修课,是专业基础课程之一, 它应用数学方法和相关科学技术知识解决实际中提出的专门问题,为决策者选择最佳方案提供定量依据的科学。
(二)课程目标
通过本课程的学习,使学生掌握运筹学各主要分支的模型、基本概念与理论、主要算法和应用,并能在计算机上应用各种优化软件包熟练地操作解决一些实际应用案例,从而为学生进一步从事该方向的学习与研究工作打下坚实的基础,并能使学生在相关部门的学习实践中提高解决实际问题的能力。
三、教学内容和要求
(一)理论教学的内容及要求
第1章 绪论
§1.1 运筹学的概况
1. 运筹学的由来和发展
2. 运筹学的性质与特点
3. 运筹学的主要内容
4. 运筹学的发展趋势
§1.2 运筹学的数学模型
1. 线性规划模型
2. 随机规划模型
3. 网络分析模型
本章教学重点和难点
重点:运筹学的主要内容和数学模型。
难点:随机规划模型。
本章教学基本要求
详细介绍运筹学所包括的主要分支、应用范围和发展趋势,详细讲解运筹学常用的几个数学模型。
第2章 线性规划
§2.1 线性规划问题
1. 线性规划问题举例
2. 线性规划模型
§2.2 可行区域与基本可行解
1. 图解法
2. 可行区域的几何结构
3. 基本可行解及线性规划的基本定理
§2.3 单纯形方法
1. 单纯形方法
2. 单纯形表
§2.4 初始解
1. 两阶段法
2. 关于单纯形法的几点说明
§2.5 对偶性与对偶单纯形法
1. 对偶线性规划
2. 对偶理论
3. 对偶单纯形法
§2.6 灵敏度分析
1. 改变价值向量
2. 改变右端向量
本章教学重点和难点
重点:线性规划可行区域的几何结构,基本可行解及线性规划基本定理,单纯形方法,两阶段法,对偶性及对偶单纯形法。
难点:线性规划可行区域的几何结构,基本可行解及线性规划基本定理,两阶段法,对偶性。
本章教学基本要求
1. 使学生掌握线性规划数学三种模型,线性规划的基本概念及基本理论;
2. 熟练掌握单纯行方法和两阶段法;
3. 掌握对偶理论及对偶单纯行方法;
4.了解灵敏度分析。
第3章 整数线性规划
§3.1 整数线性规划问题
1.整数线性规划问题举例
2.解整数线性规划问题的困难性
§3.2 Gomory割平面法 )
1. Gomory割平面法的基本思想
2. Gomory割平面法计算步骤
§3.3 分枝定界法
1. 分枝定界法的基本思想
2. 分枝定界法计算步骤
本章教学重点和难点
重点:Gomory割平面法和分枝定界法。
难点:Gomory割平面法和分枝定界法的基本思想。
本章教学基本要求
1. 让学生了解整数线性规划的一些实际背景及常用算法;
2. 让学生学会用Gomory割平面法求解整数线性规划问题;
3. 让学生学会用分枝定界法求解整数线性规划问题。
第4章 非线性规划
§4.1 基本概念
1.非线性规划问题
2.非线性方法概述
§4.2 凸函数和凸规划
1. 凸函数及其性质
2. 凸规划及其性质
§4.3 一维搜索方法
1.0.618法
2.Newton法
§4.4 无约束最优化方法
1. 无约束问题的最优性条件
2. 最速下降法
3. 共轭方向法
§4.5 约束最优化方法
1. 约束最优化问题的最优性条件
2. 简约梯度法
3. 惩罚函数法
本章教学重点和难点
重点:凸规划及其性质,无约束优化问题的最优性条件及其最速下降法,约束优化问题的最优性条件。
难点:K-T条件。
本章教学基本要求
1. 掌握有关非线性规划的基本概念、理论和某些重要算法;
2. 让学生详细了解凸规划及其性质;
3.掌握无约束和约束优化问题的最优性条件及其相应的求解方法。
第5章 动态规划
§5.1 最优化原理
1.多阶段决策问题及例
2.用递推法解最短路线问题
3.最优化原理
§5.2 确定性的定期多阶段决策问题
1. 旅行售货员问题
4. 排序问题
§5.3确定性的不定期多阶段决策问题
1.最优线路问题
本章教学重点和难点
重点:用递推法解最短路线问题,最优化原理,旅行售货员问题,最优线路问题。
难点:最优线路问题。
本章教学基本要求
1. 使学生掌握多阶段决策问题的最优化原理和求解方法;
2. 使学生学会用最优化原理求解旅行售货员问题和最优线路问题的方法。
第6章 网络分析
§6.1 图与子图 )
1.图与网络
2.关联矩阵和邻接矩阵
3. 子图
§6.2 图的连通与割集
1. 图的连通
2. 图的割集
§6.3 树与支撑树
1. 树及其基本性质
2. 支撑树及基本性质
§6.4 最小树
1. 最小树及其性质
2. 求最小树Kruskal算法
3. Dijkstra算法
§6.5最短有向路
1. 最短有向路方程
2. 求最短有向路的Dijkstra算法
§6.6 最大流
1. 最大流最小割定理
2. 最大流算法
§6.7 最小费用流
1. 最小费用流算法
2. 特殊的最小费用流——运输问题
§6.8 最大对集
1. 二分图对集
2. 二分图的最大基数对集
3. 二分网络的最大权对集——分派问题
本章教学重点和难点
重点:图的连通与割集,最小树、最大流、最小费用流和最大对集的基本性质及其求解方法。
难点:有关割集的理论,最小费用流算法,二分图的最大权对集。
本章教学基本要求
1. 了解有关图与网络的基本概念;
2. 熟练掌握最小树、最大流、最小费用流和最大对集的基本理论及其求解方法。
第7章 排队论
§7.1 随机服务系统概论
1.随机服务系统的基本组成部分
2.几个常用的概率分布和最简单流
本章教学重点和难点
重点:几个常用的概率分布和最简单流。
难点:几个常用的概率分布和最简单流。
本章教学基本要求
1. 了解几个常用的概率分布;
2. 掌握最简单流。
第8章 决策分析
§8.1 决策分析的基本概念
1.决策分析的基本概念
2.决策的数学模型和例子
§8.2 确定性决策分析
1. 进行确定性决策分析的条件和步骤
2. 盈亏平衡分析决策法
3. 计分模型决策法
§8.3 风险型决策分析
1. 进行风险型决策分析的基本条件和方法
2. 决策树
§8.4 不确定型决策分析 1. 不确定型决策分析的条件和例子
2. 不确定型决策分析的基本方法
§8.5 效用函数和信息的价值
1. 效用函数及其应用
2. 信息的价值
本章教学重点和难点
重点:确定性、风险型和不确定型决策分析的基本方法。
难点:不确定型决策分析。
本章教学基本要求
1. 掌握决策模型;
2. 了解确定性、风险型和不确定型决策分析的基本条件和方法;
3.了解效用函数和信息价值。
第9章 对策论
§9.1 引言
1.对策论发展简史
2.对策模型
3. 例子
§9.2 对策的解 1. 矩阵对策及其解的概念
2. 对抗对策的解
3. 人对策的平衡局势
§9.3 矩阵对策的解法
1. 矩阵对策的简化
2. 线性规划方法
§9.4 合作对策
1. 特征函数
本章教学重点和难点
重点:对策的解,矩阵对策的解法 ,特征函数。
难点: 特征函数。
本章教学基本要求
1. 掌握对策问题,各种对策的解;
2. 学会矩阵对策的两种解法。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第1章:绪论 |
2 |
2 |
|
|
|
|
|
|
第2章:线性规划 |
20 |
18 |
|
|
2 |
|
|
|
第3章:整数线性规划 |
5 |
5 |
|
|
|
|
|
|
第4章:非线性规划 |
16 |
15 |
|
|
1 |
|
|
|
第5章:动态规划 |
4 |
4 |
|
|
|
|
|
|
第6章:网络分析 |
14 |
13 |
|
|
1 |
|
|
|
第7章: 排队论 |
1 |
1 |
|
|
|
|
|
|
第8章:决策分析 |
3 |
3 |
|
|
|
|
|
|
第9章:对策论 |
3 |
3 |
|
|
|
|
|
|
合 计 |
68 |
64 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、课程论文等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+课程论文成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1. 刁在筠等编《运筹学》(第二版), 高等教育出版社,2001年.
(二)主要参考书目
1.《运筹学》,钱颂迪,清华大学出版社,1987年
2.《线性规划》,张建中,许绍吉,科学出版社,1997年
“数据库及应用”教学大纲
教研室主任: 赵京东 执笔人:叶传秀
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数据库及应用
课程编号:06201312
英文名称:Introduction to Database System
课程类型:专业方向限选课
总 学 时:68 理论学时:51 实验学时:17 课外学时:0
学 分:4
开设专业:信息与计算科学
先修课程:数据结构(06200511)
二、课程任务目标
(一)课程任务
数据库技术是计算机科学技术中发展最快的领域之一,也是应用最广的技术之一。数据库技术是计算机科学的重要分支,数据库技术和数据库系统已经成为计算机信息系统的核心技术和重要基础。《数据库及应用》是本科信息与计算专业和统计学等相关专业的专业主干课程,是数据库系统的第一门课程。
(二)课程目标
在学完本课程之后,学生能够:
1. 使学生系统地掌握数据库系统的基本原理和基本技术。;
2. 能熟练使用SQL语言在某一个数据库管理系统上进行数据库操作;
3. 掌握数据库设计方法和步骤,具有设计数据库模式以及开发数据库应用系统的基本能力;
三、教学内容和要求
(一)理论教学的内容及要求
第一章 概论
第一节 数据库系统概述
1. 理解数据、数据库、数据库管理系统、数据库系统的概念;
2. 了解数据管理技术的产生和发展过程;
3. 理解库系统的特点;
第二节 数据模型
1.了解数据模型的基本概念;
2.理解数据模型的组成要素;
3. 掌握概念模型的基本概念及其主要建模方法ER方法;
4. 了解最常用的数据模型;
第三节 数据库系统结构
1. 了解数据库系统模式的概念;
2. 掌握数据库系统的三级模式结构;
3. 掌握数据库的二级映象功能与数据独立性;
4. 掌握数据库系统外部的体系结构;
第四节 数据库系统的组成
1. 掌握数据库系统的组成部分;
2. 理解数据库系统的各组成部分的特点;
第五节 数据库技术的研究领域
1.了解数据库管理软件的研制;
2. 理解数据库设计的方法、设计工具、设计理论、数据模型和数学建模;
3. 理解关系的规范化理论和关系数据理论;
本章教学重点:
1.概念模型的基本概念及其主要建模方法ER方法;
2.关系数据模型的相关概念、数据库系统三级模式和两层映像的体系结构、数据库系统的逻辑独立性和物理独立性等;
3.对于如何通过ER方法描述现实世界的概念模型要做到能够举一反三的程度。
本章教学难点:
掌握数据库领域大量的基本概念;数据模型及数据库系统的体系结构。
第二章 关系数据库
第一节 关系模型概述
1.了解关系数据库理论产生和发展的过程;
2.了解关系数据库产品的发展及沿革;
3.掌握关系模型的三个组成部分;
4.掌握关系的三类完整性约束和概念;
第二节 关系数据结构
1.关系数据结构的基本概念及形式化定义;
2.掌握关系模式的表示方法;
3.了解关系数据库产品的发展与沿革;
第三节 关系的完整性
1.掌握关系模型中三类完整性约束的概念;
第四节 关系代数
1.理解常用的集体运算的概念和运算方法;
1.掌握常用的关系代数的相关概念及运算方法;
第五节 关系演算
1.了解元组关系演算语言ALPHA;
2.了解域关系演算语言QBE;
3.能够用关系演算语言完成各种数据操纵;
本章教学重点:
1.关系模型的组成及各部分所包括的内容;
2.关系数据结构及其形式化定义;
3.关系的三类完整性约束;
4.关系代数运算;
本章教学难点:
1.关系代数;
第三章 关系数据库标准SQL
第一节 SQL概述
1.了解SQL语言的发展过程;
2.掌握SQL语言的特点;
第二节 数据定义
1.掌握SQL数据定义语句格式;
2. 掌握SQL语言中基本表操作和索引操作的方法;
第三节 查询
1.掌握利用SQL语言完成对数据库中单表查询、连接查询、嵌套查询、集合查询的查询方法;
2.掌握对数据库进行复杂查询的方法;
第四节 数据更新
1.掌握数据库中数据插入、修改、删除的方法;
第五节 视图
1.了解视图的特点;
2.掌握基于视图的定义、查询、更新等基本操作;
3.理解视图的作用;
第六节 数据控制
1.掌握数据控制的功能与实现;
2.掌握SQL授权功能的操作方法;
3.掌握SQL收回权限的功能
第七节 嵌入式SQL
1.了解引入嵌入式SQL的原因;
2.理解嵌入式SQL的一般形式;
3.理解嵌入式SQL语句与主语言之间的通信;
4.理解不用游标和使用游标的SQL语句;
5.了解动态SQL;
本章教学重点:
1.SQL语言的特点;
2.使用SQL语言完成对数据库的查询、插入、删除、更新等基本操作;
3.SQL语言中的数据控制;
本章教学难点
1.使用SQL语言完成对数据库的查询、插入、删除、更新等基本操作;
2.嵌入式SQL;
第四章 关系系统及其查询优化
第一节 关系系统
1.了解关系系统的定义和分类;
2.掌握最小关系的系统、关系上完备的系统、全关系型的关系系统等基本概念;
3.了解全关系系统的十二条准则;
第二节 关系系统的查询优化
1.了解查询优化的必要性;
2.理解查询优化的准则和关系代数等价变换规则;
3.掌握关系系统的查询优化方法;
4.理解代数优化算法和物理优化算法;
本章教学重点:
1. 关系系统、最小关系的系统、关系上完备的系统、全关系型的关系系统等基本概念;
2. 关系系统的查询优化方法;
本章教学难点:
代数优化算法和物理优化算法
第五章 关系数据理论
第一节 问题的提出
1.理解数据依赖的基本概念;
2.掌握关系模式的形式化和简化定义;
第二节 规范化
1.掌握函数依赖及其相关的基本概念;
2.掌握范式的概念和1NF、2NF、3NF、4NF的定义;
3.掌握关系模式规范化的含义、基本思想和步骤;
第三节 数据依赖的公理系统
1.了解Armstrong公理系统;
2.掌握函数依赖闭包、函数依赖集的计算方法;
第四节 模式的分解
1.了解三种模式分解的等价定义;
2.掌握四种模式分解的方法;
3.理解模式分解的算法;
本章教学重点:
1.关系的形式化定义;
2.数据依赖的基本概念;
3.范式的概念和四类范式的定义;
4.关系模式的规范化。
本章教学难点:
1.各个级别范式的关系及其证明;
2. 模式分解的方法;
第六章 数据库设计
第一节 数据库设计概述
1.了解数据库设计的特点;
2.掌握数据库设计的方法和基本步骤;
第二节 需求分析
1.了解需求分析的任务;
2.掌握需求分析的方法;
3.掌握数据字典的用途和内容;
第三节 概念结构设计
1.理解概念结构设计的概念和特点;
2.掌握概念结构设计的方法与步骤;
3.了解数据抽象的概念和用途;
4.掌握E-R图的设计方法和分E-R图的集成;
第四节 逻辑结构设计
1.掌握逻辑结构设计的任务和步骤;
2.掌握E-R图向关系模型的转换方法;
3.掌握优化数据模型的方法;
第五节 数据库的物理设计
1.了解数据库物理设计的内容和评价;
2.掌握DBMS常用存取方法;
3.了解数据库的存储结构;
4.了解物理结构的评价方法;
第六节 数据库实施
1.理解数据库实施的工作内容及其实现方法;
第七节 数据库运行与维护
1.了解DBA的工作内容;
2.理解数据库的重组织和重构造
本章教学重点:
1.数据库设计的基本步骤;
2.数据库设计过程中数据字典的内容;
3.数据库设计各个阶段的具体设计内容、设计描述、设计方法;
4.E-R图的设计;
本章教学难点:
1.E-R图的设计;
2.数据模型的优化;
第七章 数据库恢复技术
第一节 事务的基本概念
1.掌握事务的基本概念和ACID性质;
2.理解事务的定义方法;
第二节 数据库恢复概述
1.了解故障产生的原因和影响;
2.了解数据库管理系统对故障的对策;
第三节 故障的种类
1.掌握故障的种类;
2.了解各种故障的定义和产生的原因;
第四节 恢复的实现技术
1.理解恢复机制涉及的关键问题;
2.掌握数据转储及其转储方法;
3.掌握登记日志文件的内容和原则;
第五节 恢复策略
1.掌握各种故障的恢复方法和步骤;
2.掌握拓扑排序的思想及其算法实现;
3.理解关键路径及其相关概念;
4.掌握关键路径的思想及其实现过程;
5.理解关键路径的求解算法;
第六节 具有检查点的恢复技术
1.理解检查点技术;
2.掌握利用检查点的恢复策略;
第七节 数据库镜像
1.理解数据库镜像的概念和用途;
第八节 Oracle的恢复技术
1.了解Oracle的恢复技术;
本章教学重点:
1.事务的基本概念和事务的ACID性质;
2.数据库恢复的实现技术;
3.日志文件的内容及作用;
4.登记日志文件所要遵循的原则;
5.具有检查点的恢复技术;
本章教学难点:
1.日志文件的使用;
2.系统故障恢复策略;
第八章 并发控制
第一节 并发控制概述
1.了解并发控制机制的任务;
2.了解并发操作带来的数据不一致性;
第二节 封锁
1.了解封锁的概念;
2.掌握基本封锁类型;
3.掌握基本锁的相容矩阵;
第三节 封锁协议
1.掌握封锁协议的概念;
2.掌握三级封锁协议的区别;
第四节 活锁和死锁
1.掌握避免活锁的方法;
2.掌握解决死锁的方法;
第五节 并发调度的可串行性
1.了解什么样的并发操作调度是正确的;
2.保证并发操作的调度是正确的方法;
第六节 两段锁协议
1.掌握两段锁协议的基本概念和内容;
2.理解两段锁协议与死锁、可串行性的关系;
第七节 封锁的粒度
1.掌握封锁粒度的概念;
2.掌握多粒度封锁方法;
3. 掌握多粒度封锁协议的相容控制矩阵;
4.了解具有意向锁的多粒度封锁方法的封锁过程;
第八节 Oracle的并发控制
1.了解Oracle采用封锁技术保证并发操作的可串行性的方法;
2.了解Oracle锁的种类;
本章教学重点:
1.并发操作可能产生数据不一致性的情况及其确切定义;
2.封锁的类型,不同封锁类型的性质和定义;
3.相关的相容控制矩阵;
4.封锁协议、封锁粒度;
5. 粒度封锁方法,多粒度封锁协议的相容控制矩阵;
本章教学难点:
1. 两段锁协议与死锁、可串行性的关系;
2. 具有意向锁的多粒度封锁方法的封锁过程;
第九章 数据库安全性
第一节 计算机安全性概论
1.了解计算机系统的三类安全性问题 ;
2.掌握TDI/TCSEC标准的基本内容;
3.掌握TCSEC/TDI安全级别划分;
第二节 数据库安全性控制
1.掌握实现数据库安全性控制的常用方法;
2.掌握实现数据库安全性控制的相关技术;
第三节 统计数据库安全性
1.了解统计数据库的特点和安全问题;
第四节 选择排序Oracle数据库的安全性措施
1.理解ORACLE的安全措施;
本章教学重点:
1. TDI/TCSEC标准的基本内容;
2.C2级DBMS、B1级DBMS的主要特征;
3. 实现数据库安全性控制的常用方法和技术;
4.数据库中自主存取控制方法和强制存取控制方法;
本章教学难点:
1.Mac机制中确定主体能否存取客体的存取规则;
第十章 外部排序
第一节 完整性约束条件
1.了解数据库的完整性约束条件;
2.了解完整性约束条件的分类;
第二节 完整性控制
1.掌握DBMS完整性控制机制的三个方面;
2.了解关系系统三类完整性的实现;
3.理解参照完整性的实现;
第三节 Oracle的完整性
1.了解Oracle中的实体完整性;
2.了解Oracle中的参照完整性;
3.了解败者树的构造方法Oracle中用户定义的完整性;
本章教学重点:
DBMS完整性控制机制的三个方面;
本章教学难点:
RDBMS实现参照完整性的策略;
(二)实践教学的内容及要求
1. 语言实验
熟悉实验环境;掌握创建数据库基本表和修改基本表结构;建立,删除索引的方法;能够对数据库基本表增,删,改数据;完整性约束验证。
2. 数据查询
熟悉SQL查询的理论知识和SQL语言,掌握利用SQL进行各种数据库查询操作。
3. 视图定义与操纵实验
熟悉视图操作,掌握定义视图和利用视图进行查询,更新操作的方法。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:绪论 |
2 |
2 |
|
|
|
|
|
|
第二章:关系数据库 |
3 |
3 |
|
|
|
|
|
|
第三章:关系数据库标准语言 |
12 |
6 |
|
6 |
|
|
|
|
第四章:关系系统及其查询优化 |
17 |
6 |
|
11 |
|
|
|
|
第五章:关系数据理论 |
8 |
8 |
|
|
|
|
|
|
第六章:数据库设计 |
6 |
6 |
|
|
|
|
|
|
第七章:数据库恢复技术 |
4 |
4 |
|
|
|
|
|
|
第八章:并发控制 |
4 |
4 |
|
|
|
|
|
|
第九章:数据库安全技术 |
6 |
6 |
|
|
|
|
|
|
第十章:数据库完整性 |
6 |
6 |
|
|
|
|
|
|
合 计 |
68 |
51 |
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方式:闭卷;
总评成绩=期中成绩×0.2+平时(包括作业、上机实验考核,总分为10分)+期末成绩×0.7
六、主要教材及教学参考书目
(一)主要教材
1.萨师煊,王珊:数据库系统概论(第三版) ,高等教育出版社,2000
(二)主要参考书目
1.Date C J, An Introduction to Database System (Ed.7), Addison-Wesley,2000
2.王珊,陈红:《数据库系统原理教程》, 清华大学出版社,2000
“编译原理”教学大纲
教研室主任:赵京东 执笔人:叶传秀
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:编译原理
课程编号:06201412
英文名称:Compile Principle
课程类型:专业方向限选课
总 学 时:68 理论学时:51 实验学时:17 课外学时:
学 分:4
开设专业:信息与计算科学专业
先修课程:C语言()17000210;离散数学(06200411);数据结构(06200511)
二、课程任务目标
(一)课程任务
《编译原理》课程是计算机类各专业的一门重要专业基础课,是为培养计算机应用系统和软件系统开发的人才的需要而设置的。本课程的任务是使学生掌握编译系统的结构、工作流程及编译程序各部分的设计原理和实现技术。具有设计、实现、分析和维护等方面的初步能力。通过学习该课程,使学生掌握编译程序的基本原理及方法,为以后从事应用软件和系统软件的开发打下一定的理论及实践基础。
(二)课程目标
在学完本课程之后,学生能够:
1. 掌握编译系统的结构、工作流程及编译程序各部分的设计原理和实现技术;
2. 具有设计、实现、分析和维护等方面的初步能力;
3. 掌握编译程序的基本原理及方法,为以后从事应用软件和系统软件的开发打下一定的理论及实践基础。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 引论
第一节 什么叫编译程序
1.了解编译程序的基本概念及其发展历程;
2.掌握编译程序与解释程序的特点和区别;
第二节 编译过程概述
1.掌握编译程序的工作过程及其各个阶段的功能;
第三节 编译程序的结构
了解编译程序的总体框架;
了解遍、编译前端、编译后端的概念;
第四节 编译程序与程序设计环境
了解程序设计环境;
了解Apse程序设计环境的组成;
第五节 编译程序的生成
1.理解T型图;
2.理解编译程序的移植;
本章教学重点:
1.编译程序的过程及其每个阶段的功能;
2.编译程序的总体框架;
本章教学难点:
1.编译程序的移植;
第二章 高级语言及其语法描述
第一节 程序语言的定义
1.理解语法的定义;
2.理解语义的定义;
3.了解常见的语法范畴;
第二节 高级语言的一般特性
1.了解高级语言的分类;
2.了解Fortran语言、Pascal语言、Ada语言、Java语言的程序结构;
3.了解常见的数据类型与操作;
4.了解常见的语句、表达式和控制结构;
第三节 程序语言的语法描述
1.掌握闭包、正则闭包的概念;
2.理解文法的定义;
3.掌握上下文无关文法的定义;
4.理解文法的相关概念;
5.掌握语法分析树的构造方法;
6.掌握文法二义性的判别;
7.理解乔姆斯基对文法的分类及每类文法的特点;
本章教学重点:
1.上下文无关文法;
2.语法分析树;
3.文法二义性;
本章教学难点:
1. 上下文无关文法;
2. 乔姆斯基对文法的分类及每类文法的判别方法;
第三章 词法分析
第一节 对于词法分析器的要求
1.理解解单词符号的分类;
2.理解单词的种及其二元式表示;
第二节 词法分析器的设计
1.了解词法分析的输入与预处理;
2.理解单词符号的识别方法-超前搜索;
3.掌握状态转换图构造方法;
4.理解状态转换图的实现方法;
第三节 正规表达式与有限自动机
1.理解正规式、正规集的概念;
2.掌握正规式、正规集转换方法;
3.理解DFA的定义与表示方法;
4.理解NFA的定义与表示方法;
5.掌握NFA的确定化方法;
6.掌握正规文法与有限自动机的转换方法;
7.掌握正规集与有限自动机的转换方法;
8.掌握有限自动机的化简方法;
第四节 词法分析器的自动生成
1.了解描述词法分析器的语言LEX;
2.理解LEX的实现;
本章教学重点:
1.状态转换图构造方法;
2.正规式、正规集的转换方法;
3.DFA、NFA的定义与表示
4.NFA的确定化方法;
5.正规文法与有限自动机的转换方法;
6.正规集与有限自动机的转换方法;
7.有限自动机的化简;
本章教学难点
1.NFA的确定化方法;
2.正规文法与有限自动机的转换方法;
3.正规集与有限自动机的转换方法;
4.有限自动机的化简;
第四章 语法分析-自上而下分析
第一节 语法分析器的功能
1.了解语法分析在编译程序中的地位;
2.了解语法分析的两种方法;
第二节 自上而下分析面临的问题
1.了解自上而下分析的过程;
2.理解自上而下分析面临的困难;
第三节 LL(1)分析法
1.掌握消除左递归的方法;
2.掌握提取公共因子的方法;
3.掌握First集、Follow集、Select集的求解方法;
4.掌握LL(1)文法的判别方法;
第四节 递归下降分析程序构造
1.掌握递归下降分析程序的构造方法;
第五节 预测分析程序
1.理解预测分析程序的工作过程;
2.掌握预测分析表的构造方法;
第六节 LL(1)分析中的错误处理
1.了解LL(1)分析中错误处理的方法;
本章教学重点:
1.LL(1)文法的判别;
2.非LL(1)文法转化为LL(1)文法的方法;
3.递归下降分析程序的构造方法。
4.预测分析表的构造方法。
本章教学难点:
1.LL(1)文法的判别;
2.非LL(1)文法转化为LL(1)文法的方法;
3.递归下降分析程序的构造方法。
第五章 语法分析-自下而上分析
第一节 自下而上分析基本问题
1.理解归约、规范归约、推导、规范推导的概念;
2.理解句柄、短语、直接短语的概念;
3.掌握归约、推导的过程;
4.了解栈与语法分析树在语法分析中的作用;
第二节 算符优先分析
1.理解算符优先文法、素短语的概念;
2.掌握FirstVt集、LastVt集的计算方法;
3.掌握算符优先表的构造方法及其分析方法;
4.理解优先函数的定义和构造方法;
第三节 LR分析法
1.理解LR分析的思想;
2.掌握LR(0)项目集规范族的构造方法和LR(0)分析表的构造方法;
3.掌握SLR项目集规范族及其分析表的构造方法;
4.掌握规范LR项目集规范族及其分析表的构造方法;
5.理解LALR项目集规范族及其分析表的构造方法;
6.掌握利用LR分析表对给定输入串进行LR分析的工作过程
第四节 语法分析器的自动产生工具YACC
1.了解编译程序自动产生工具YACC;
本章教学重点:
1.FirstVt集、LastVt集的计算方法;
2.算符优先表的构造方法及其分析方法;
3.LR(0)项目集规范族的构造方法及其分析表的构造方法;
4.SLR项目集规范族及其分析表的构造方法;
5.规范LR项目集规范族及其分析表的构造方法;
6.利用LR分析表对给定输入串进行LR分析的工作过程。
本章教学难点:
1.算符优先表的构造方法及其分析方法;
2.LR(SLR、规范LR、LALR)项目集规范族的构造方法及其分析表的构造方法;
3.利用LR分析表对给定输入串进行LR分析的工作过程。
第六章 属性文法和语法制导翻译
第一节 属性文法
1.理解属性文法的概念;
2.掌握综合属性、继承属性的概念;
3.了解属性在语法分析中传递过程;
第二节 基于属性文法的处理方法
1.掌握依赖图的构造方法;
2.理解树遍历的属性计算方法;
3.掌握抽象语法树的构造方法;
第三节 S-属性文法的自下而上计算
1.理解S属性文法的定义;
2.掌握S-属性的计算方法;
第四节 L-属性文法和自顶向下翻译
1.理解L属性文法的定义;
2.了解文法的翻译模式的描述方法;
3.理解L属性文法在自顶向下分析中的实现过程;
第五节 自下而上计算继承属性
1. 理解L属性文法的定义;
2.理解继承属性在自下而上分析中的实现;
本章教学重点:
1.语法制导翻译的概念;
2.依赖图的构造方法;
3.抽象语法树的构造方法;
4.S-属性的计算方法;
5.L属性文法在自顶向下分析中的实现过程。
本章教学难点:
1.S-属性的计算方法;
2.L属性文法在自顶向下分析中的实现过程;
3. 自下而上计算继承属性。
第七章 语义分析和中间代码产生
第一节 中间语言
1.掌握中间代码的表示方法;
2.掌握后辍式、三元式、间接三元式、四元式的表示方法;
第二节 说明语句
1.了解说明语句的特点;
2.理解说明语句的语法制导翻译;
第三节 赋值语句的翻译
1.掌握简单表达式的语义分析和代码产生的过程;
2.掌握简单赋值语句的语义分析和代码产生的过程;
3.掌握数组元素赋值语句的语义分析和代码产生的过程;
第四节 布尔表达式的翻译
1.掌握布尔型表达式的语义分析和代码生成的过程;
2.掌握条件语句的语义分析和代码产生的过程;
第五节 控制语句的翻译
1.掌握控制流语句的语义分析和代码产生的过程;
2.掌握标号和Goto语句的语义分析和代码产生的过程;
3.掌握Case语句的语义分析和代码产生的过程;
第六节 过程调用
1.理解过程调用的语义分析和代码产生的过程;
第七节 类型检查
1.了解多态性处理的思想;
2.理类型检查的实现过程;
本章教学重点:
1.简单赋值语句的翻译;
2.布尔型表达式的翻译;
3.IF、 While、Goto、Case、For语句的翻译;
4.数组元素赋值语句的翻译。
本章教学难点:
1.布尔型表达式的地址回填;
2.数组元素的赋值语句的翻译;
3.过程调用的实现;
4.生成各种语句中间代码的语义子程序。
第十章 优化
第一节 概述
1.了解代码优化的重要性和相应的原则;
2.掌握常用的代码优化技术;
第二节 局部优化
1.掌握划分基本块的算法;
2.理解基本块的DAG表示;
3.掌握局部优化的实现方法;
第三节 循环优化
1.理解循环优化的思想;
2.掌握代码外提、强度削弱、删除归纳变量等循环优化的方法;
本章教学重点:
1.局部优化技术;
2.循环优化技术。
本章教学难点:
1.局部优化的实现;
2. 循环优化的实现。
(二)实践教学的内容及要求
实验1. 词法分析实验
了解C语言的编程环境及调试过程和词法分析的任务,理解有限自动机的相关理论,掌握单词符号的识别方法。
实验 2.语法分析实验
了解C语言的编程环境及调试过程和语法分析的任务,理解递归下降分析和LL(1)分析的理论知识,掌握语法单位生成的实现算法。
实验3.语义分析和中间代码生成实验
了解C语言的编程环境及调试过程和语义分析的任务,理解属性方法和语法制导翻译的相关知识,掌握语法单位翻译成中间代码的方法。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:引论 |
2 |
2 |
|
|
|
|
|
|
第二章:高级语言及其语法描述 |
6 |
6 |
|
|
|
|
|
|
第三章:词法分析 |
14 |
8 |
|
6 |
|
|
|
|
第四章:语法分析-自上而下 |
9 |
6 |
|
3 |
|
|
|
|
第五章:语法分析-自下而上分析 |
13 |
10 |
|
3 |
|
|
|
|
第六章:属性文法和语法制导翻译 |
8 |
8 |
|
|
|
|
|
|
第七章:语义分析与代码产生 |
13 |
8 |
|
5 |
|
|
|
|
第十章:优化 |
3 |
3 |
|
|
|
|
|
|
合 计 |
68 |
51 |
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方式:闭卷;
总评成绩=期中成绩×0.2+平时(包括作业、上机实验考核,总分为10分)+期末成绩×0.7。
六、主要教材及教学参考书目
(一)主要教材
1.陈火旺等著《编译原理》(第3版),国防工业出版社,2000年。
(二)主要参考书目
1.秦振松《编译原理与编译程序构造》, 东南大学出版社1997年版;
2.陈意云等《编译原理》,高等教育出版社2003年版。
“操作系统”教学大纲
教研室主任:赵京东 执笔人:叶传秀
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:操作系统
课程编号:06201512
英文名称:Computer Operating System
课程类型:专业方向限选课
总 学 时:51 理论学时:51 实验学时:0 课外学时:0
学 分:3
开设专业:信息与计算科学
先修课程:数据结构(06100511)
二、课程任务目标
(一)课程任务
《操作系统》是信息与计算科学专业的重要课程之一。通过本课程的学习,使学生全面、系统地掌握计算机操作系统的基本概念、基本技术和基本方法;掌握计算机操作系统的组成和各部分的功能;了解计算机操作系统的发展特点、设计的基本原理和方法;对常用操作系统(Dos.Windows.Unix)会进行基本的操作使用。
(二)课程目标
在学完本课程之后,学生能够:
1.掌握操作系统的基本原理、实现机制和基本算法;
2.掌握计算机操作系统的组成和各部分的功能
3.具有设计、实现、分析和维护等方面的初步能力;
三、教学内容和要求
(一)理论教学的内容及要求
第一章 操作系统引论
第一节 操作系统的目标和作用
1.理解操作系统的目标;
2.理解操作系统的作用;
3.了解推动操作系统发展的主要动力;
第二节 操作系统和发展过程
1.了解操作系统的发展历程;
2.掌握脱机输入、输出方式的概念和优点;
3.掌握多道批处理系统的概念和特征;
4.掌握分时系统和实时系统的概念和特征;
第三节 操作系统的基本特性
1.理解并发、并行、共享、虚拟的概念;
2.掌握操作系统的基本特性;
第四节 操作系统的主要功能
1.掌握操作系统的主要功能;
2.理解各个管理模块的任务;
第五节 操作系统的结构设计
1.理解软件、软件工程的概念;
2.了解传统操作系统的结构;
本章教学重点:
1.脱机输入、输出方式;
2.多道批处理系统、分时系统和实时系统的概念和特征;
3.操作系统的基本特性;
4.掌握操作系统的主要功能。
本章教学难点:
1.多道批处理系统、分时系统和实时系统的概念和特征;
2.传统操作系统的结构。
第二章 进程管理
第一节 进程的基本概念
1.理解程序的概念和特征;
2.掌握前趋图的画法;
3.掌握进程的概念和特征;
4.掌握进程的状态和进程控制块的概念;
第二节 进程控制
1.理解进程图;
2.掌握进程的创建过程及其产生的原因;
3.掌握进程终止的过程及其产生的原因;
4.掌握进程阻塞与唤醒的过程及其产生的原因;
5.掌握进程挂起与唤醒的过程及其产生的原因;
第三节 进程同步
1.理解进程同步的基本概念;
2.掌握信号量机制及其PV原语操作;
第四节 经典进程的同步问题
1.掌握利用信号量机制解决生产者、消费者问题的方法;
2.掌握利用信号量机制哲学家就餐问题的方法;
3.掌握利用信号量机制解决读者写者问题的方法;
第五节 管程机制
1.理解管程的概念;
2.理解利用管程机制解决生产者、消费者问题的方法;
第六节 进程通信
1.理解进程通信的类型和通信方式;
2.掌握消息缓冲队列通信机制实现通信的方法;
第七节 线程
1.掌握线程的概念和与进程的区别;
2.理解线程的状态;
3.理解线程间的同步与通信过程;
4.理解线程控制的实现方法;
本章教学重点:
1.进程的控制;
2.进程同步机制的实现与经典问题的解决;
3.利用消息缓冲队列通信机制实现进程通信。
本章教学难点:
1. 进程同步机制的实现与经典问题的解决;
2. 利用管程机制实现进程同步;
3.线程及其线程控制。
第三章 处理机调度与死锁
第一节 处理机调度的基本概念
1.掌握作业调度、进程调度和中级调度的概念和任务;
2.理解调度队列模型;
3.理解选择调度的方式和调度算法的准则;
第二节 调度算法
1.掌握先来先服务、短作业优先调度算法;
2.掌握响应比优先调度算法;
3.掌握时间片轮转的调度算法;
第三节 实时调度
1.理解实时调度的基本条件;
2.掌握常见的实时调度算法;
第四节 多处理机调度
1.了解多处理器系统的类型;
2.理解多处理器系统中的进程分配与调度方式;
第五节 产生死锁的原因和必要条件
1.掌握产生死锁的原因;
2.掌握产产生死锁的四个必要条件;
3.理解处理死锁的方法;
第六节 预防死锁的方法
1.掌握预防死锁的方法;
2.理解系统的安全状态;
3.掌握利用银行家算法避免死锁的方法;
第六节 死锁的检测与解除
1.掌握死锁分配图的画法和死锁定理;
2.掌握死锁解除的方法;
本章教学重点:
1.进程调度的方法;
2.死锁的原因、必要条件、和预防方法;
3.利用银行家算法避免死锁。
本章教学难点
1.进程调度;
2.利用银行家算法避免死锁;
3.实时调度的实现。
第四章 存储器管理
第一节 程序的装入和链接
1.理解程序的装入的概念和装入方式;
2.理解程序的链接的概念和链接方式;
第二节 连续分配方式
1.掌握连续分配的方式和各自的特点;
2.理解对换的概念及其实现过程;
第三节 基本分页存储管理方式
1.掌握基本分页存储管理中的数据结构;
2.掌握基本分页存储管理中地址变换机构的工作原理;
第四节 基本分段存储管理方式
1.掌握基本分段存储管理中的数据结构;
2.掌握基本分段存储管理中地址变换机构的工作原理;
3. 掌握段页式存储管理中地址变换机构的工作原理;
4.掌握分段与分页的区别;
第五节 虚拟存储器的基本概念
1.了解虚拟存储器的特征;
2.理解局部性原理;
第六节 请求分页存储管理方式
1.理解请求分页中的硬件支持;
2.理解内存分配策略和分配算法;
3.掌握请求分页存储管理中地址变换机构的工作原理;
第七节 页面置换算法
1.掌握最佳、FIFO、LRU页面置换算法;
2.理解Clock转换算法和其它的置换算法;
第八节 请求分段存储管理方式
1.理解请求分段中的硬件支持;
2.理解分段的共享和保护的实现;
3.掌握请求分段存储管理中地址变换机构的工作原理;
本章教学重点:
1.连续分配的存储管理方式;
2.基本分页和请求分页的存储管理方式;
3.页面置换算法;
4.基本分段和请求分段的存储管理方式。
本章教学难点:
1.分页、请求分页、分段、请求分段和段页式存储管理试中的地址变换机构的工作原理;
2.页面置换算法。
第五章 设备管理
第一节 I/O系统
1.了解I/O设备的类型、与控制器的接口;
2.掌握设备管理器的基本功能和组成;
3.理解I/O通道的概念和类型;
4.了解常见的系统总线;
第二节 I/O控制方式
1.掌握四种常见的I/O控制方式;
2.理解每种控制方式的特点
第三节 缓冲管理
1.理解缓冲引入的原因;
2.理解单缓冲、双缓冲、循环缓冲和缓冲池的工作特点;
第四节 设备分配
1.理解设备分配中的数据结构;
2.了解设备分配时应考虑的因素;
3.掌握设备独立性的概念;
4.掌握Spooling技术及其特点;
第五节 设备处理
1.理解设驱动程序的功能和特点;
2.理解设备驱动程序的处理过程;
3.理解中断处理程序的处理过程;
第六节 磁盘存储器管理
1.了解磁盘的工作原理;
2.掌握磁盘的调度算法;
3.理解磁盘的高速缓存;
本章教学重点:
1.I/O控制方式;
2.设备独立性与Spooling技术;
3.磁盘的调度算法。
本章教学难点:
1.缓冲区技术;
2.设备独立性与Spooling技术。
第六章 文件管理
第一节 文件和文件系统
1.理解文件、记录、数据项的概念;
2.了解文件类型和文件系统模型;
3.掌握基本的文件操作;
第二节 文件的逻辑结构
1.理解文件的逻辑结构和物理结构;
2.理解文件逻辑结构的类型;
3.掌握顺序文件和索引文件的组织形式;
4.了解直接文件和哈希文件;
第三节 外存分配方式
1.理解连续分配、链式分配及其特点;
2.掌握索引分配方式和特点;
第四节 目录管理
1.理解目录管理的要求;
2.理解文件控制块和索引结点的结构;
3.掌握目录结构的组织方式;
4.了解目录查询技术;
第五节 文件存储空间的管理
1. 掌握常用的文件存储空间的管理方法;
第六节 文件共享与文件保护
1.理解基于索引结点和利用符号实现文件共享的方法;
2.理解磁盘容错技术;
第七节 数据一致性控制
1.理解事务的概念和事务操作的实现;
2.了解检查点的作用;
3.理解并发控制技术;
4.了解重复数据的一致性问题;
本章教学重点:
1.文件的定义和基本操作;
2.目录管理与目录结构的组织方式;
3. 文件存储空间的管理方法。
本章教学难点:
1.目录管理与目录结构的组织方式;
2. 外存分配方式。
第七章 操作系统的接口
第一节 联机命令接口
1.掌握联机命令的类型;
2.了解键盘终端处理程序;
3.理解命令解释程序;
第二节 Shell命令语言
1.了解常见的Shell命令;
第三节 系统调用
1.掌握系统调用的概念;
2.了解系统调用的类型和实现;
第四节 Unix系统调用
1.了解Unix系统调用的类型;
2.了解被中断进程的环境保护和陷入后需处理的若干公共问题的处理方法;
第五节 图形用户接口
1.了解常见的图形用户接口;
本章教学重点:
1.联机命令的接口类型;
2.系统调用的概念与实现。
本章教学难点:
1.Shell命令语言;
2.Unix系统调用。
(二)实践教学的内容及要求
实验1. 熟悉操作系统
了解常见的系统环境Windows、Dos、Unix,掌握这些系统的操作方法。
实验2. 进程管理实验
了解常见的系统环境,理解进程管理的相关理论,掌握利用所学理论处理进程同步、进程通信等实际问题的方法。
实验 3.银行家算法实验
了解C语言的编程环境及调试过程,理解避免死锁的理论知识,掌握利用银行家算法避免死锁的实现算法。
实验4.存储器管理实验
了解C语言的编程环境及调试过程,理解分页、分段等内存分配的方法,掌握模拟内存分配的实现算法。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:操作系统引论 |
2 |
2 |
|
|
|
|
|
|
第二章:进程管理 |
9 |
8 |
|
|
1 |
|
|
|
第三章:处理机调度与死锁 |
9 |
8 |
|
|
1 |
|
|
|
第四章:存储管理 |
9 |
8 |
|
|
1 |
|
|
|
第五章:设备管理 |
8 |
8 |
|
|
|
|
|
|
第六章:文件管理 |
9 |
8 |
|
|
1 |
|
|
|
第七章:操作系统接口 |
5 |
5 |
|
|
|
|
|
|
合 计 |
51 |
47 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方式:闭卷笔试;
总评成绩=期中成绩×0.2+平时(包括作业、上机实验考核,总分为10分)+期末成绩×0.7。
六、主要教材及教学参考书目
(一)主要教材
1.汤子瀛等 著《计算机操作系统》(修订版),西安电子科技大学出版社,2001年。
(二)主要参考书目
1.张尧学,史美林著 《计算机操作系统教程(第二版)》,清华大学出版社, 2000年。
2.刘乃琦著 《计算机操作系统》,电子工业出版社,1996年。
“数值逼近”教学大纲
教研室主任:赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数值逼近
课程编号:06201612
英文名称:Numerical Approximation
课程类型:专业方向限选课
总 学 时:51 理论学时:51 实验学时:0 课外学时:0
学 分:3
开设专业:信息与计算科学
先修课程: 高等代数(06200221)
二、课程任务目标
(一)课程任务
本课程是一门信息与计算科学专业学科基础课课程。本课程的任务是使学生获得计算数学的基本思想方法和数值逼近系统的基本知识。它一方面为学生继续从事计算数学方向的学习提供一些所需的基础理论和知识,另一方面还对提高学生思维能力、开发学生智能、加强 “三基”(基础知识、基本理论、基本技能)及培养学生独立工作能力等起着重要的作用。
(二)课程目标
在学完本课程之后,学生能够:
1.掌握数值逼近的常用的基本的数值计算方法;
2.掌握数值逼近的基本理论、分析方法和原理;
3.能利用计算机解决科学和工程中的某些数值计算应用问题,增强综合运用知识的能力;
4.了解科学计算的发展方向和应用前景。
三、教学内容和要求
第一章 绪论
教学重点:绝对误差,相对误差,误差限,有效数字和可靠数字的定义和相互关系。
教学难点:有限运算下的失真现象。
第一节 什么是数值分析
1.了解数值分析的有关概念;
2.了解“四舍五入”规则和“截断”规则;
3了解有限运算下的失真现象。
第二节 误差和有效数字
1.了解误差的来源;
2.掌握绝对误差,相对误差,误差限,有效数字和可靠数字的定义的相互关系。
第三节 数制与浮点运算
1.掌握数制及浮点数的表示形式;
2.掌握浮点数的四则运算及基本定理。
第二章 函数的插值
教学重点:拉格朗日插值多项式,牛顿插值多项式,差分,差商,埃尔米特差值。
教学难点:等距节点的牛顿插值公式,埃尔米特插值。
第一节 多项式插值
1.了解多项式插值的有关概念;
2.熟练掌握拉格朗日插值多项式的计算公式;
3.理解内维尔途径构造插值多项式的方法;
4.掌握差商的定义及性质;
5.熟练掌握牛顿插值公式及余项形式。
第二节 等距节点插值和差分
1.掌握差分的定义及性质;
2.理解等距节点的牛顿插值公式。
第三节 重节点差商与埃尔米特插值
1.掌握重节点差商的概念及计算;
2.掌握埃尔米特插值的计算方法。
第四节 非多项式插值
理解非多项式插值的有关概念。
第三章 样条插值和曲线拟合
教学重点:分段插值,样条插值。
教学难点:样条插值,贝齐尔曲线。
第一节 多项式插值的龙格现象
1.了解多项式插值的龙格现象;
2.掌握分段插值的基本思想。
第二节 样条插值
1.了解样条插值的概念及常用类型;
2.理解样条插值的计算方法。
第三节 贝齐尔曲线
1.掌握贝齐尔曲线的概念及性质;
2.理解贝齐尔曲线的有关定理。
第四章 最佳逼近
教学重点:最佳一致逼近多项式,最佳平方逼近多项式,曲线拟合的最小二乘法。
教学难点:最佳一致逼近多项式,曲线拟合的最小二乘法。
第一节 C[a,b]上的最佳一致逼近
1.掌握最佳一致逼近的定义及相关定理;
2.掌握契比雪夫多项式及其性质;
3.理解里米兹算法的基本思想。
第二节 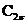 上的最佳一致逼近
上的最佳一致逼近
1.掌握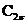 上的最佳一致逼近的特性;
上的最佳一致逼近的特性;
2.理解杰克生定理。
第三节 最佳平方逼近
1.掌握最佳平方逼近多项式的概念和计算;
2.掌握最小二乘原理作曲线拟合的方法及计算步骤。
第四节 
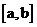 上的正交多项式
上的正交多项式
1.理解正交多项式的定义及性质;
2.掌握勒让德多项式和切比雪夫多项式的定义及性质。
第五章 数值积分
教学重点:牛顿-柯特斯公式,复化术积公式,龙贝格算法。
教学难点:外推原理,龙贝格算法。
第一节 牛顿-柯特斯公式
1.理解插值求积公式的原理和牛顿-柯特斯公式;
2.掌握梯形公式和辛卜生公式及其余项形式;
3.了解数值稳定性的概念及牛顿-柯特斯公式的数值稳定性。
第二节 提高求积公式精度的方法
1.掌握复化求积公式;
2.掌握外推原理和龙格贝算法。
第三节 非等距点的求积公式
1.理解一致系数公式的推导过程;
2.掌握高斯型求积公式的具体构造方法。
第四节 特殊积分的处理技术
理解振荡函数和奇异积分的处理方法。
第五节 多重积分
了解多重积分的计算方法。
第六章 快速傅立叶变换
教学重点:快速傅立叶变换及算法。
教学难点:快速傅立叶变换的基本思想。
第一节 傅立叶分析
掌握傅立叶级数和傅立叶变换的概念及其相关定理。
第二节 离散傅立叶变换
掌握离散傅立叶变换的基本思想。
第三节 快速傅立叶变换
掌握快速傅立叶变换及算法。
第四节 FFT在卷积中的应用
了解快速傅立叶变换在卷积中的应用。
第七章 函数方程求根
教学重点:迭代法,牛顿法,简化牛顿法。
教学难点:迭代法,牛顿法。
第一节 二分法与插值法
1.掌握二分法;
2.理解反插值法的基本思想。
第二节 迭代法
掌握迭代法的基本思想及收敛定理。
第三节 牛顿法
1.理解牛顿法的推导过程;
2.掌握牛顿法的计算公式及收敛定理。
第四节 简化牛顿法及弦割法
1.理解简化牛顿法及弦割法的推导过程;
2.掌握简化牛顿法及弦割法的计算公式;
3了解简化牛顿法及弦割法的收敛定理。
第五节 实多项式求根的林士谔-贝尔斯多夫方法
了解林士谔-贝尔斯多夫方法。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 绪论 |
4 |
4 |
|
|
|
|
|
|
第二章 函数的插值 |
6 |
6 |
|
|
|
|
|
|
第三章 样条插值和曲线拟合 |
8 |
8 |
|
|
|
|
|
|
第四章 最佳逼近 |
10 |
10 |
|
|
|
|
|
|
第五章 数值积分 |
10 |
10 |
|
|
|
|
|
|
第六章 快速傅立叶变换 |
3 |
3 |
|
|
|
|
|
|
第七章 函数方程求根 |
10 |
10 |
|
|
|
|
|
|
合 计 |
51 |
51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合。期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+期中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.蒋尔雄等《数值逼近》,复旦大学出版社,2004年。
(二)主要参考书目
1. 王仁宏著《数值逼近》,高等教育出版社,1999年。
2.马富明等《数值逼近》,吉林大学出版社,2000年。
“微分方程数值解法”教学大纲
教研室主任:郑召文 执笔人:徐伟
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:微分方程数值解法
课程编号:06201712
英文名称:Numerical Methods of Differential Equations
课程类型:专业方向限选课
总 学 时:34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算科学
先修课程:常微分方程(06200511)
二、课程任务目标
(一)课程任务
本课程为数学学院计算与信息科学专业方向限选课,为数学学院本科三年级学生第二学期所必修。
(二)课程目标
1.了解常微初值问题在工程技术中的应用,了解三类偏微分方程(描述稳定状态的椭圆型偏微分方程,描述扩散状态的抛物型偏微分方程,描述波动状态的双曲型偏微分方程)在工程技术中的广泛应用;了解微分方程数学模型中各项数学描述的物理含义;了解建立微分方程数学模型的一般方法。
2.学习常微分方程数值求解格式的构造及其稳定性分析方法。
3. 学习数值求解二阶椭圆型偏微分方程的有限元方法
4. 学习数值求解扩散偏微分方程的差分方法
5. 学习数值求解波动方程的差分方法
三、教学内容和要求
(一)理论教学的内容及要求
第一章 结论
§1微分方程
§2数值求解微分方程的意义
§3数值求解方法的概述
本章教学要求:掌握微分方程的相关概念与数值求解微分方程的意义。
第二章 常微分方程初值问题:
§1 常微分方程的若干理论
§2 单步方法
§3 线性多步方法
§4 微分方程组和刚性问题
本章教学要求:掌握线性多步方法,Runge-Kutta方法,Gear方法等计算常微分方程的计算格式,掌握相容性,稳定性,绝对稳定性概念和相互关系,理解刚性问题和辛计算格式。
第三章 差分法解边值问题
§1 解两点边值问题的差分方法
§2 解椭圆边值问题的差分方法
§3 椭圆差分方程的性态研究
本章教学要求:掌握椭圆型方程的五点、九点差分格式和有限体积法,掌握极值原理,收敛性分析和误差估计。
第四章 外推法
§1外推法的引入
§2展开式定理
§3加速收敛
§4外推法的应用
本章教学要求:掌握外推法的概念性质,理解展开式定理的内容,理解多项式外推相关概念,能够用外推方法求常微分方程初值问题。
第五章 发展方程差分方法:
§1 几个典型的发展方程
§2 扩散方程的差分化
§3 稳定性分析
§4 双曲型方程的差分化和稳定性
§5高维问题
本章教学要求:掌握抛物型方程和双曲型方程的差分方法,掌握稳定性分析包括直接法,分离变量法,最大模方法,传播因子法,掌握Courant-Friedrichs-Lewy条件和Von Neumann分析方法。
第六章 变分及泛函的极值问题
§1变分问题
§2泛函的极值问题
§3变分和泛函极值问题的近似求解
本章教学要求:理解变分问题的概念、相关性质,能够给出两点边值问题、椭圆型方程等问题的变分形式,会求与此相关的泛函的极值问题,并且能够求变分和泛函极值的近似求解。
第七章 椭圆型方程的有限元解法:
§1 解两点边值问题的有限元方法
§2 多角区域上椭圆型方程的有限元方法
§3 曲边三角形和等参元
§4有限元方法的超收敛性质简介
本章教学要求:掌握有限元计算格式的推导,掌握基本的有限元误差分析。
第八章 多重网格和区域分解算法:
§1 多重网格简介
§2 区域分解方法简介
本章教学要求:理解多重网格和区域分解的原理。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 结论 |
1 |
1 |
|
|
|
|
|
|
第二章 常微分方程初值问题 |
6 |
6 |
|
|
|
|
|
|
第三章 差分法解边值问题 |
5 |
5 |
|
|
|
|
|
|
第四章 外推法 |
2 |
2 |
|
|
|
|
|
|
第五章 发展方程差分方法 |
6 |
6 |
|
|
|
|
|
|
第六章 变分及泛函的极值问题 |
6 |
6 |
|
|
|
|
|
|
第七章 椭圆型方程的有限元解法 |
6 |
6 |
|
|
|
|
|
|
第八章 多重网格和区域分解算法 |
2 |
2 |
|
|
|
|
|
|
合 计 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
采用闭卷考试,主要以试题和其中考试、平时作业作为评分的依据,采用百分制,评分标准:1)期末考试(70%);2)期中考试(20%);3)平时作业(10%)。
六、主要教材及教学参考书目
(一)主要教材
1.李立康、於崇华、朱政华《微分方程数值解法》复旦大学出版社 1998
(二)主要参考书目
1.荣华、冯果忱《微分方程数值解法》,高等教育出版社 2001
2.Alfil Quarteroni , Alberto Valli 《Numerical Approximation of partial Deifferential Equations》, Springer-Verlag.2001
“计算机图形学”教学大纲
教研室主任:赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:计算机图形学
课程编号:06201812
英文名称:Computer Graphics
课程类型:专业方向限选课
总 学 时: 51 理论学时:34 实验学时:17 课外学时:
学 分: 3
开设专业:信息与计算专业
先修课程:C语言程序设计(17000210),解析几何(06200311),数值代数(06200911)
二、课程任务目标
(一)课程任务
计算机图形学是计算机科学与技术及其相关专业的一门专业技术基础课,它是图像处理、模式识别、CAD、CAM、CIMS、CAI、CAE、计算机绘图、计算机艺术、多媒体以及各种应用系统的重要基础。在计算机科学与技术等专业人才培养中,对提高学生的能力、素质和形成良好的知识结构都具有重要意义。
理解和掌握计算机图形学中最基本、最广泛应用的概念、原理、理论和算法以及基本技术和方法。
(二)课程目标
1.了解计算机图形学的发展、应用以及当前国际国内研究的热点和重要成果。
2.理解计算机图形系统的组成、功能、工作原理以及GKS图形国际标准等。
3.掌握计算机图形学中最基本、最广泛应用的概念、原理、理论和算法以及基本技术和方法;掌握简单图形系统的开发技术。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 图形设备、系统和应用
了解计算机图形学和图像处理的研究对象、应用领域、发展历史和研究内容,以及图形和图像的开发工具。
本章重点:计算机图形学的研究内容,计算机图形学的应用领域。
本章难点 :计算机图形学算法研究的发展。
第一节 计算机图形学的发展历史
1.了解计算机图形学起源;
2.了解计算机图形学硬件设备的发展;
3.了解计算机图形学算法研究的发展。
第二节 计算机图形学的研究内容及应用领域
1.了解图形用户界面、CAD/CAM、科学计算可视化、地理信息系统、娱乐、计算机艺术、虚拟现实、逆向工程。
第二章 计算机图形系统
教学目标:了解计算机图形系统的软硬件发展,理解各种视频设备的工作原理,掌握光栅扫描、随机扫描系统的结构,掌握各种输入设备和硬拷贝设备。掌握Windows操作系统下的图形程序开发方法和OpenGL绘图程序。
本章重点:计算机图形设备和图形软件及图形标准。
本章难点 :Windows操作系统下的图形程序开发方法及OpenGL的绘制流程和原理。
讲授内容
第一节 计算机图形系统概述
1.了解计算机图形外部设备(图形显示设备、计算机图形输入设备、计算机图形输出设备);
2.了解计算机图形软件(几何造型平台、CAD/CAM软件、计算机动画软件、科学计算机可视化软件);
3.了解图形标准(图形标准的产生与发展历史、DXF图形交换格式、CGM计算机图形元文件、IGES图形交换标准、STEP产品模型数据交换标准)。
第二节 Windows操作系统下图形程序开发方法介绍
1.了解Windows应用程序执行模式;
2.了解基本的Windows应用程序;
3.理解Windows图形环境介绍(设备上下文DC、使用设备上下文、Windows图形程序开发方法)。
第三节 OpenGL介绍
1.了解OpenGL的背景情况
2.理解OpenGL的主要功能
3.掌握OpenGL的绘制流程和原理
4.掌握使用C++开发OpenGL绘图程序的基本方法
5.了解OpenGL的缓冲区(颜色缓存、深度缓存、模板缓存、累积缓存)。
第三章 基本光栅图形生成技术
第一节 光栅图形学概述及线的生成算法
1.掌握直线的生成算法(数值微分法、Bresenham算法);
2.掌握圆弧的生成算法(圆的基本绘制算法、中点画圆法、椭圆的绘制)。
第二节 区域的填充
1.掌握扫描线算法(有序边表的扫描线算法、边界标志算法);
2.掌握种子填充算法;
3.掌握区域图案填充算法。
第三节 文字的生成(自学)
1.了解点阵字符;
2.了解矢量字符。
第四节 用C++生成基本图形
1.理解图形设备接口;
2.理解C++绘图方法。
第五节 用OpenGL生成基本图形
1.掌握用OpenGL生成点;
2.掌握用OpenGL生成直线(绘制直线、绘制折线);
3.掌握用OpenGL生成区域图形(区域图形绘制、区域图形的填充、多边形面的绘制);
4.掌握用OpenGL生成字符(生成英文字体、生成中文字体);
5.理解OpenGL的颜色缓冲区。
第四章 图形变换
第一节 几何变换
1.理解几何变换的概念和作用;
2.掌握基本几何变换(平移变换、缩放变换、旋转变换);
3.掌握组合几何变换与齐次坐标(齐次坐标、组合变换)。
第二节 坐标变换
1.掌握坐标变换的概念与作用;
2.掌握基本坐标变换方法;
3.掌握齐次坐标下的坐标变换方法。
第三节 显示变换
1.掌握窗口到视区的变换;
2.掌握透视投影变换;
3.掌握平行投影变换;
4.掌握视坐标系与视变换;
5.理解窗口到三维空间的变换。
第四节 裁剪
1.掌握裁剪的概念与作用(视景体、何时裁剪、视景体的规范化);
2.掌握线段的裁剪(二维直线的裁剪、三维直线段的裁剪);
3.掌握多边形裁剪(Sutherland_Hodgman算法、Weiler_Atherton算法)。
第五节 OpenGL坐标变换机制
1.理解OpenGL中与变换有关的数据结构(矩阵、矩阵堆栈);
2.理解OpenGL中的ModelView变换机制;
3.理解OpenGL中的Model变换使用方法(直接定义变换矩阵、用OpenG中库函数);
4.理解OpenGL中的View变换使用方法;
5.理解OpenGL的投影;
6.理解OpenGL的深度缓冲区;
7.理解OpenGL中的反变换;
第五章 交互绘图技术
教学目标
了解设计用户对话时应注意的内容,掌握输入设备的逻辑分类和各种输入模式,掌握各种交互式构图技术。
本章重点
Windows、MFC、OpenGL对交互式绘图的支持与实现。
本章难点
橡皮筋技术、各种操作的交互式控制方法。
讲授内容
第一节 窗口系统、事件驱动模式
1.了解窗口;
2.了解事件驱动模式
3.了解Windows下基于消息的事件驱动编程
4.了解MFC中的事件驱动编程
5.了解状态与事件结合程序控制模式
第二节 交互式的显示控制技术
1.理解场景充满窗口的控制方法
2.掌握旋转操作的交互控制方法
3.掌握平移操作的交互控制方法
第三节 交互式的图形生成技术
1.理解交互式绘图概述
2.掌握坐标的输入技术
3.掌握橡皮筋技术
第四节 交互式的图形编辑技术
1.了解交互式图形编辑的基本方法
2.掌握图形元素拾取技术
第六章 真实感图形的生成技术
教学目标
了解借助数学、物理、计算机等学科的知识在计算机二维显示屏上产生三维场景的真实逼真图像、图形的过程;理解消隐、光照、纹理映射、阴影生成、反走样技术; 掌握用OpenGL生成真实感图形。
本章重点
用OpenGL生成真实感图形时简单光照模型、物体材质、纹理映射的应用。
本章难点
消隐、光照、纹理映射、阴影生成、反走样技术。
讲授内容
第一节 消隐技术
1.了解消隐技术;
2.掌握多面体隐藏线消除(消除自隐藏线、隐藏面、深度测试、 包围盒测试);
3.理解Z缓冲器消隐算法。
第二节 光照技术
1.理解简单光照模型;
2.了解光线跟踪与辐射度方法。
第三节 物体表面细节的模拟
1.了解颜色纹理映射技术(纹理函数定义、映射函数定义、纹理映射的实施);
2.理解环境映射技术。
第四节 阴影的生成及图形反走样技术
1.了解影域多边形方法;
2.了解Z缓冲方法;
3.了解反走样技术。
第五节 用OpenGL生成真实感图形
1.了解OpenGL的光照环境设置方法;
2.了解OpenGL的物体材料特性的设置;
3.了解OpenGL的纹理映射方法。
第七章 曲线与曲面
教学目标
了解曲线、曲面生成方法的发展;理解多边形表面表示方法、样条表示和各种样条、样条曲线和曲面的显示方法及其他实体表示方法;掌握用OpenGL生成NURBS曲线和曲面。
本章重点
用OpenGL生成NURBS曲线和曲面。
本章难点
实用图形系统中常用的曲线曲面生成方法。
讲授内容
第一节 曲线曲面入门
1.了解曲线、曲面的表示形式;
2.理解曲线曲面的光滑连接(位置连续、斜率连续、曲率连续)。
第二节 三次样条曲线曲面
1.了解三次样条函数(物理背景、三次样条函数的数学定义、用型值点处的一阶导数表示插值三次样条函数—m关系式);
2.理解三次样条曲线。
第三节 Bézier曲线和曲面
1.理解Bézier曲线;
1.理解Bézier曲面(Bézier曲面片的定义、C0连续的Bézier组合曲面(位置连续)、C1连续的Bézier组合曲面(导矢连续))。
第四节 B样条曲线和曲面
1.理解均匀B样条曲线;
2.理解均匀B样条曲面。
第五节 非均匀有理B样条曲线曲面(自学)
1.理解非均匀B样条曲线曲面(非均匀B样条基函数、非均匀B样条曲线的实现、非均匀三次B样条曲面);
2.理解有理B样条曲线。
第六节 用OpenGL生成曲线和曲面
1.了解 用OpenGL生成NURBS曲线;
2.了解用OpenGL生成NURBS曲面;
3.了解用OpenGL生成裁剪NURBS曲面。
(二)实践教学的内容及要求
1.TC下画图
了解TC下的画图方法,使用图形函数绘制运动的三角形,每个顶点遇到屏幕边界后反弹。
2.基本图元绘制算法
掌握圆的基本绘制算法、中点画圆法、椭圆的绘制
3.区域填充
掌握扫描线算法(有序边表的扫描线算法、边界标志算法)
掌握种子填充算法;用种子填充算法(或扫描线填充算法)填充任一多边形域
4.真实感图形显示
给出一(运动的)物体表面的颜色(图案),以及光源位置,以某个角度观察,显示在二维平面上。
5.Bezier曲线的绘制
理解Bezier曲线的生成原理,对给出n个(运动的)控制点,绘制贝塞尔曲线。
6.交互绘图技术
了解OpenGL交互式绘图的基本方法
7.三次样条曲线曲面
理解Bézier曲面(Bézier曲面片的定义、C0连续的Bézier组合曲面(位置连续)、C1连续的Bézier组合曲面(导矢连续));理解均匀B样条曲线;理解均匀B样条曲面。
8.综合绘图
全面了解,并初步掌握OpenGL交互式绘图,具有初级编制绘图程序的能力。
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 图形设备、系统和应用 |
1 |
1 |
|
|
|
|
|
|
第二章 计算机图形系统 |
1 |
1 |
|
|
|
|
|
|
第三章 基本光栅图形生成技术 |
28 |
18 |
|
10 |
|
|
|
|
第四章 图形变换 |
2 |
2 |
|
|
|
|
|
|
第五章 交互绘图技术 |
7 |
1 |
|
6 |
|
|
|
课程设计(自定) |
第六章 真实感图形的生成技术 |
8 |
7 |
|
1 |
|
|
|
|
第七章 曲线与曲面 |
4 |
4 |
|
|
|
|
|
|
合 计 |
51 |
34 |
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方法:闭卷;
成绩评定的方法:总评成绩=期末考试(60%)+上机与实验(10%)+课程设计(20%)+平时与作
业(10%)
六、主要教材及教学参考书目
(一)主要教材
1. 孙家广主编:《计算机图形学》,高教出版社1998年出版
(二)主要参考书目
1. 陆润民主编:《计算机图形学教程》,清华大学出版社2003年出版
2. 焦永和主编:《计算机图形学教程》,北京理工大学出版社2004年出版
“多媒体技术”教学大纲
教研室主任: 赵京东 执笔人:赵京东
一、课程基本信息
开课单位:数学科学
课程名称:多媒体技术
课程编号:06201912
英文名称:Multimedia Technical
课程类型:专业方向限选课
总 学 时: 34 理论学时:34 实验学时: 课外学时:
学 分:2
开设专业:信息与计算专业
先修课程:计算机文化基础(17000110)
二、课程任务目标
(一)课程任务
多媒体技术把计算机技术的交互性和可视化的真实感结合起来,使其应用渗透到各个领域。因此本课程的目的与任务是使学生通过本课程的学习,理解多媒体技术的基本概念和主要功能,了解如何进行多媒体软件开发和多媒体制造,学会多媒体系统的制作技术及方法,掌握多媒体创作工具软件的使用,掌握多媒体计算机系统的工作原理,掌握常用的多媒体工具软件的使用方法,为以后从事多媒体软件系统的开发及应用打下基础。
(二)课程目标
掌握多媒体技术的基本概念与基本知识:多媒体、位图、图形、图像、;掌握视频、音频获取、实时处理技术、声音图像的压缩编码技术。掌握多媒体计算机的软硬件平台与多媒体开发工具的使用。了解多媒体作品的开发步骤及方法与技术,能进行简单的多媒体编程与作品的制作。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 多媒体技术概述
1. 把握多媒体技术的基本概念与基本知识
2. 掌握几种常见的媒体元素
3. 了解多媒体技术的发展过程、发展前景及其意义
4. 了解多媒体技术研究的主要内容
第二章 音频信息的获取及处理
1. 了解数字化声音获取的方法及处理过程
2. 了解声音信息压缩编码的规则
3. 掌握音频卡的工作原理及分类标准
4. 掌握各种声音文件区别及制作方法
第三章 视频信息的获取及处理
1. 掌握图像的彩色空间表示及其转换
2. 掌握视频信息获取技术及实时处理技术
3. 了解图像的压缩编码
4. 了解图像文件格式及其转换
第四章 媒体计算机硬件系统结构
1. 了解光盘的工作原理
2. 了解VCD及DVD工作原理
3. 掌握触摸屏、扫描仪、数码相机的基本常识
4. 了解多媒体处理器的几种分类
5. 了解多媒体总线及多媒体个人计算机
第五章 媒体计算机软件结构
1. 了解多媒体软件系统层次划分
2. 了解几种可支持多媒体的操作系统
3. 掌握几种多媒体素材制作软件
4. 了解多媒体应用软件
第六章 多媒体素材制作
1. 掌握几种多媒体素材制作的工具软件
2. 掌握Flash MX的基本操作;
3. 掌握 Photoshop的基本操作;
4. 掌握制作多媒体素材的方法及过程
第七章 超文本和超媒体
1. 掌握超文本和超媒体的基本概念
2. 掌握超文本和超媒体的体系结构
3. 掌握超文本和超媒体的应用
4. 了解超文本和超媒体存在的问题和发展前景
5. 了解智能超媒体系统
第八章 多媒体计算机的应用技术
1. 掌握多媒体电子出版物的创作流程
2. 掌握多媒体会议系统的组成及工作原理
3. 了解多媒体数据库及基本内容检索
第九章 多媒体作品创作
1. 掌握Authorware应用
2. 掌握动画制作及网页设计
(二)实践教学的内容及要求
(上机时间学生自我安排)
1.音频信息、视频信息的获取及处理
了解视频卡和声频卡的功能
2.媒体计算机软件结构
掌握常见媒体播放软件的获取、安装、应用。
3.动画素材获取
掌握Flash MX的常用工具,编制简单的动画;
4.图形、图像素材的获取与处理
掌握PhotoShop的基本工具,学会简单的图像处理技术(公用工具的使用、文件及基本菜单、遮罩的使用方法、图像的旋转、倾斜、透视和扭曲变形、改变图像大小和分辨率、图像的格式转换、分色和合成技术、浮雕、柔焦、水纹、旋涡、二维和三维扭曲特殊效果、图像的输出、扫描和模式转换)
5.超文本和超媒体
掌握超文本的访问方式和超文本系统的特性、超文本系统与操作工具
6.多媒体节目著作系统
了解创作多媒体节目的软件平台,了解多媒体著作系统的基本功能。
7.多媒体作品创作
了解Authorware多媒体著作系统的功能特点;掌握Authorware图标的使用、Authorware的变量与函数的使用、Authorware常用函数的使用、在Authorware中播放MIDI音乐、播放256色动画时的颜色失真处理
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 多媒体技术概述 |
2 |
2 |
|
|
|
|
|
|
第二章 音频信息的获取及处理 |
2 |
2 |
|
|
|
|
|
|
第三章 视频信息的获取及处理 |
4 |
4 |
|
|
|
|
|
|
第四章 媒体计算机硬件系统结构 |
2 |
2 |
|
|
|
|
|
|
第五章 媒体计算机软件结构 |
2 |
2 |
|
|
|
|
|
|
第六章 多媒体素材制作 |
12 |
12 |
|
|
|
|
|
|
第七章 超文本和超媒体 |
2 |
2 |
|
|
|
|
|
|
第八章 多媒体计算机的应用技术 |
4 |
4 |
|
|
|
|
|
课程设计(自定) |
第九章 多媒体作品创作 |
4 |
4 |
|
|
|
|
|
|
合 计 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方法:闭卷;
成绩评定的方法:总评成绩=期末考试(70%)+课程设计(20%)+平时与作业(10%)
六、主要教材及教学参考书目
(一)主要教材
1. 胡晓峰 吴玲达 老松杨 司光亚等 编著,《多媒体技术教程》,人民邮电出版社。
(二)主要参考书目
1. 袁承武 袁丽娜 编著,《多媒体技术基础》,北京航空航天大学出版社。
2. 林福宗 编著,《多媒体技术基础》,清华大学版社。
数学模型教学大纲
教研室主任:郑召文 执笔人:白玉真
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数学建模
课程编号:06202013
英文名称:Mathematical Model
课程类型:专业基础课
总 学 时:34 理论学时:34 实验学时:0 课外学时:
学 分:2
开设专业:信息与计算数学
先修课程:数学分析(06200131) 高等代数(06200221) 常微分方程(06200611)
二、课程任务目标
(一)课程任务
数学模型课程是信息与计算数学专业的必修课,是专业基础课程之一, 主要讲授如何应用数学知识将实际问题翻译成数学问题,以及数学求解的结果如何翻译回到实际中去。
(二)课程目标
通过该课程的学习,要使学生系统地获得数学建模的基本知识、基本理论和方法,培养和训练学生的数学建模素质;引导学生思考数学与科学、数学与现实之间的关系,培养学生用数学方法解决实际问题的能力,培养学生的动手能力和创新精神。
三、教学内容和要求
(一)理论教学的内容及要求
第1章 建立数学模型
1.1 从现实对象到数学模型
1.2 数学建模的重要意义
1.3 建模示例之一 椅子能在不平的地面上放稳吗
1.4 建模示例之二 商人们怎样安全过河
1.5 建模示例之三 如何预报人口的增长
1.6 数学建模的基本方法和步骤
1.7 数学模型的特点和分类
1.8 数学建模能力的培养
本章教学重点和难点
重点:数学模型与数学建模
难点:数学建模的基本方法和步骤
本章教学基本要求
1. 了解数学模型与数学建模过程;
2. 理解数学建模的基本方法和步骤;
3. 掌握几个简单的智力问题模型。
第二章 初等模型
2.1 公平的席位分配
2.4 汽车刹车距离
2.5 划艇比赛的成绩
2.7 实物交换
2.8 核军备竞赛
2.10 量纲分析和无量纲化
本章教学重点和难点
重点:初等方法建模的思想与方法
难点:初等方法建模的思想与方法
本章教学基本要求
1. 掌握Q值法和d’Hondt方法;
2. 掌握类比法和比例法进行数学建模;
3. 理解无差别曲线的特点,掌握无差别曲线进行数学建模。
第三章 简单的优化模型
3.1存贮模型
3.4最优价格
3.6 消费者的选择
3.7 冰山运输
本章教学重点和难点
重点:存贮模型
难点:存贮模型
本章教学基本要求
1. 了解优化模型的建模建立思想;
2. 理解优化模型的一般意义;
3. 掌握优化模型求解方法;
4. 能够解决简单的经济批量问题和连续问题模型。
第五章 微分方程模型
5.1 传染病模型
5.2 经济增长模型
5.3 正规战与游击战
5.4 药物在体内的分布与排除
5.6 人口的预测和控制
5.7 烟雾的扩散与消失
本章教学重点和难点
重点:微分方程方法建模
难点:微分方程方法建模。
本章教学基本要求
1. 掌握微分方程建模的基本方法;
2. 掌握用数值方法求解微分方程的方法。
第六章 稳定性模型
6.1 捕鱼业的持续收获
6.2 军备竞赛
6.3 种群的相互竞争
6.4 种群的相互依存
6.5 食饵-捕食者模型
本章教学重点和难点
重点:微分方程平衡点的稳定性分析
难点:微分方程定性与稳定性理论
本章教学基本要求
1. 掌握利用变化关系建立微分方程模型;
2. 掌握利用微分方程定性与稳定性理论分析变化趋势;
3. 掌握两个种群的三种不同的关系模型。
第七章 差分方程模型
7.1 市场经济中的蛛网模型
7.3 差分形式的阻滞增长模型
7.4 按年龄分组的种群增长
本章教学重点和难点
重点:差分方程平衡点的稳定性分析
难点:差分方程的稳定性理论
本章教学基本要求
1. 了解差分法基本理论;
2. 深刻理解差分法基本特点;
3. 熟练掌握差分法建模方法。
第八章 离散模型
8.1 层次分析模型
8.2 循环比赛的名次
8.4 效益的合理分配
本章教学重点和难点
重点:层次分析法建模
难点:层次分析法建模
本章教学基本要求
1. 理解层次分析法建模的基本特点;
2. 掌握层次分析法建模的基本方法;
3. 掌握竞赛图及其性质;
4. 掌握效益合理分配的Shapley值方法。
第九章 概率模型
9.2 报童的诀窍
9.3 随机存贮策略
9.5 随机人口模型
本章教学重点和难点
重点:概率方法建模
难点:随机变量和随机分布概念的灵活应用
本章教学基本要求
1. 掌握简单的随机模型的建模方法;
2. 了解概率分布、期望、方差等知识在建模问题中的应用。
第十章 统计回归模型
10.1 牙膏的销售量
10.3 酶促反应
10.5 教学评估
本章教学重点和难点
重点:统计回归建模的基本思路和方法
难点:统计回归模型的建立
本章教学基本要求
1. 掌握统计回归建模的基本方法;
2. 了解统计回归模型在实际工作中的应用。
第十一章 马氏链模型
11.1 健康与疾病
11.3 基因遗传
本章教学重点和难点
重点:马氏链模型的建立
难点:状态转移概率矩阵
本章教学基本要求
1. 掌握马氏链模型建立的方法;
2. 掌握正则链和吸收链的特点和性质;
3. 了解马氏链模型的广泛应用。
(二)实践教学的内容及要求
1. Matlab 入门
1.1 变量与函数
1.2 数组
1.3 矩阵
1.4 Matlab 编程
1.5 实验作业
教学重点和难点
重点:Matlab 编程
难点:Matlab 编程
教学基本要求
1. 了解Matlab的各种命令;
2. 掌握Matlab 编程的方法和步骤。
2. 优化模型
2.1 优化问题的基本思想和基本算法
2.2 Matlab 优化工具箱
2.3 用Matlab求解优化问题
2.4 实验作业
教学重点和难点
重点:Matlab 优化工具箱
难点:用Matlab求解优化问题
教学基本要求
1. 了解优化问题的基本思想和基本算法;
2. 掌握用Matlab求解优化问题。
3. 微分方程
3.1 求简单的微分方程的解析解
3.2 求微分方程的数值解
3.3 实验作业
教学重点和难点
重点:用Matlab 求微分方程的解析解和数值解
难点:用Matlab 求微分方程的解析解和数值解
教学基本要求
1. 学会用Matlab 求简单微分方程的解析解;
2. 学会用Matlab 求微分方程的数值解。
4. 计算机模拟
4.1 模拟的概念
4.2 计算机模拟实例
4.3 实验作业
教学重点和难点
重点:计算机模拟的基本过程和方法
难点:计算机模拟的基本过程和方法
教学基本要求
1. 掌握计算机模拟的基本过程和方法。
5. 回归分析
5.1 回归分析的基本理论
5.2 求解回归分析问题
5.3 实验作业
教学重点和难点
重点:求解回归问题的步骤和方法
难点:求解回归问题的步骤和方法
教学基本要求
1. 了解回归分析的基本内容;
2. 掌握用数学软件求解回归分析问题。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第1章: 建立数学模型 |
3 |
2 |
|
|
1 |
|
|
|
第2章:初等模型 |
4 |
3 |
|
|
1 |
|
|
|
第3章:简单的优化模型 |
4 |
3 |
|
|
1 |
|
|
|
第5章:微分方程模型 |
3 |
2 |
|
|
1 |
|
|
|
第6章:稳定性模型 |
3 |
2 |
|
|
1 |
|
|
|
第7章:差分方程模型 |
3 |
3 |
|
|
|
|
|
|
第8章:离散模型 |
4 |
3 |
|
|
1 |
|
|
|
第9章:概率模型 |
3 |
2 |
|
|
1 |
|
|
|
第10章:统计回归模型 |
3 |
3 |
|
|
|
|
|
|
第11章:马氏链模型 |
4 |
3 |
|
|
1 |
|
|
|
合 计 |
34 |
26 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、课程论文等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+课程论文成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.姜启源等编《数学模型》(第三版), 高等教育出版社,2003年.
(二)主要参考书目
1.雷功炎编著《数学模型讲义》,北京大学出版社1999年版;
2. 杨启帆主编《数学建模》,高等教育出版社2005年版。
“实变函数论”教学大纲
教研室主任:张克梅 执笔人:刘树冬
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:实变函数论
课程编号:06202113
英文名称:Theory on Real Variable Functions
课程类型:(请按我校教学计划安排表中的课程类型进行规范填写,即公共基础课、学科基础课、专业基础课、教育理论与技能基础课、专业方向限选课、专业任选课、综合素质公选课等七类)
总 学 时:34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算数学
先修课程:数学分析(06200131)
二、课程任务目标
(一)课程任务
本课程是一门信息与计算数学专业基础必修课程。本课程的任务是使学生从本质上把握Lebesgue测度与积分,掌握Lebesgue测度与积分的基本性质,理解Lebesgue积分在可积函数类,极限交换次序及微积分基本定理等方面相对于Riemann积分的优越性,培养学生分析解决数学问题的能力,提高学生的数学素养。
(二)课程目标
在学完本课程之后,学生能够:
1.掌握Lebesgue测度与积分的定义及基本性质;
2.理解Lebesgue积分在可积函数类,极限交换次序及微积分基本定理等方面相对于Riemann积分的优越性,加深对数学分析的理解;
3.利用有关知识解决一定数量的习题;
三、教学内容和要求
(一)理论教学的内容及要求
引言
1.理解Riemann积分的局限性;
2.了解Lebesgue积分的初步思想。
第一章 集合
§1.1 集合 集合的运算
1.了解集合的定义,掌握集合的运算规律。
§1.2 映射 集合的对等
1.了解映射的定义及基本性质;
2.理解集合对等的概念,掌握Bernstein定理;
3.Bernstein定理是本节的重点,也是难点。
§1.3 可列集与不可列集 集合的基数
1.了解可列集与不可列集的定义。
2.理解集合的基数的定义,这是本节的重点,也是难点。
§1.4 可列集的判定
1.了解可列集的几个常见例子;
2.掌握可列集的判断方法。
§1.5 连续势集的判断
1.了解连续势集的几个常见例子;
2.掌握连续势集的判断方法。
第二章 点集
§2.1  空间 区间 距离
空间 区间 距离
了解 空间及区间的定义;
空间及区间的定义;
2.理解距离,邻域及极限的定义,这是本节的重点;
3.掌握Bolzano-Weierstrass定理,这是本节的难点。
§2.2 内点与开集
理解内点,外点及边界点的定义;
理解开集的定义及性质,这是本节的重点。
§2.3 聚点与闭集
理解聚点与孤立点的定义,这是本节的难点;
2.理解闭集的定义,掌握闭集与开集的对偶关系,这是本节的重点。
§2.4 开集和闭集的构造
1.理解并掌握 中开集与闭集的构造,这是本节的重点,也是难点;
中开集与闭集的构造,这是本节的重点,也是难点;
2.了解 中开集与闭集的构造。
中开集与闭集的构造。
§2.5 点集间的距离 有界闭集的性质
1.了解点集间的距离的定义及性质;
2.理解并掌握Borel有限覆盖定理,这是本节的重点,也是难点。
§2.6 完备集 Cantor集
1.理解完备集及自密集的定义;
2.理解并掌握Cantor集的构造方法及性质。
第三章 测度
§3.1 引言
1.了解Jordan可测集的定义。
§3.2 Lebesgue外测度
1.理解并掌握Lebesgue外测度的定义及性质;
2.了解外测度的开集逼近。
§3.3 有界的Lebesgue可测集
1.理解并掌握有界Lebesgue可测集的定义;
2.了解开集与闭集的可测性;
3.理解并掌握有界可测集的运算性质,这是本节的重点,也是难点。
§3.4 无界的Lebesgue可测集
1.理解并掌握可测集的定义及运算性质,这是本节的重点;
2.理解并掌握可测集的构造,这是本节的难点;
3.了解常见的可测集的例子。
§3.5 不可测集的例
1.了解不可测集的构造方法。
§3.6 集合的乘积
1.了解集合的乘积的定义;
2.理解并掌握乘积集的测度的运算规律,这是本节的重点。
第四章 可测函数
§4.1 广义实函数及相关的集合
1.了解广义实函数的定义;
2.理解并掌握下方图形及特征函数的定义
§4.2 Lebesgue可测函数的定义
1.理解并掌握可测函数的定义及性质。
§4.3 可测函数与简单函数
1.了解简单函数的定义及运算性质;
2.理解并掌握简单函数与可测函数的关系,这是本节的重点,也是难点。
§4.4 可测函数的某些性质
1.理解并掌握可测函数的一些重要性质。
§4.5 Egoroff定理
1.理解并掌握Egoroff定理及其证明,这是本节的重点,也是难点。
§4.6 可测函数列的依测度收敛
1.理解依测度收敛的定义;
2.理解并掌握Lebesgue定理及Riesz定理,这是本节的重点,也是难点。
§4.7 可测函数与连续函数
1.了解连续函数的定义及性质;
2.理解并掌握Lusin定理及其证明,这是本节的重点,也是难点;
3.了解Lusin定理的其他形式。
第五章 可测函数的积分
§5.1 Lebesgue积分的定义及初等性质
1.理解并掌握可测函数的积分的定义过程,这是本节的重点;
2.了解积分的初等性质;
3.理解并掌握积分的绝对连续性。
§5.2 Lebesgue积分与Riemann积分的关系
1.理解并掌握二者的关系。
§5.3 逐项积分定理
1.理解并掌握Levi定理,Fatou引理,Lebesgue控制收敛定理,这是本节的重点,也是难点;
2.了解Lebesgue积分在处理极限交换问题上的相对于Riemann积分的优越性。
§5.4 Fubini定理
1.了解截面定理;
2.理解并掌握Fubini定理,这是本节的重点,也是难点;
3.了解Lebesgue积分在处理积分次序交换问题上的相对于Riemann积分的优越性。
§5.5 p幂可积函数
1.了解p幂可积函数的定义及性质。
第六章 微分与Lebesgue不定积分 Riemann-Stieltjes积分
§6.1 单调函数的微分性质
1.了解Vitali覆盖定理;
2.理解并掌握单调函数的微分性质,这是本节的重点,也是难点。
§6.2 有界变差函数
1.了解可求长曲线的定义;
2.理解并掌握有界变差函数的定义及性质,这是本节的重点。
§6.3 绝对连续函数与Lebesgue不定积分
1.理解绝对连续函数的定义及性质;
2.掌握不定积分与微分的关系,这是本节的重点;
3.了解Lebesgue积分的分部积分公式与换元积分公式。
§6.4 Riemann-Stietjes积分
1.了解R-S积分的定义及性质;
2.理解连续函数关于有界变差函数的R-S积分。
(二)实践教学的内容及要求
无
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
引言 |
2 |
2 |
|
|
|
|
|
|
第一章:集合 |
5 |
4 |
|
|
1 |
|
|
|
第二章:点集 |
5 |
4 |
|
|
1 |
|
|
|
第三章:测度 |
5 |
4 |
|
|
1 |
|
|
|
第四章:可测函数 |
6 |
5 |
|
|
1 |
|
|
|
第五章:可测函数的积分 |
6 |
5 |
|
|
1 |
|
|
|
第六章:微分与Lebesgue不定积分 Riemann-Stieltjes积分 |
5 |
4 |
|
|
1 |
|
|
|
合 计 |
34 |
28 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核办法:闭卷。
成绩评定办法:总成绩=平时成绩×10%+期中考试成绩×20%+期末考试成绩×70%。
六、主要教材及教学参考书目
(一)主要教材
1.郭大钧等《实变函数与泛函分析(上)》,山东大学出版社,2004年。
(二)主要参考书目
1.程其襄等《实变函数与泛函分析基础》,高等教育出版社,2003年。
2.江泽坚等《实变函数论》,高等教育出版社,1994年。
“复变函数”教学大纲
教研室主任:张克梅 执笔人:李傅山
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:复变函数
课程编号:06202213
英文名称:Complex Analysis
课程类型:专业必修课
总 学 时:34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算数学
先修课程:数学分析(06200131)
二、课程任务目标
(一) 课程任务
《复变函数》是一门重要的数学基础课,它不仅是《数学分析》的后续课程,而且也与其他
数学分支有着密切的关系,同时在其它自然科学方面(如电磁学、流体学、理论物理等)有着广泛的应用。通过本课程的学习,使学生掌握复变函数的基本理论和方法,培养学生具有较强的分析问题和解决问题的能力,为学生将来能将复变函数的思想和方法灵活应用到理论研究和应用中去打下良好的专业基础。
(二)课程目标
在学完本课程之后,学生能够:
1.通过对复变函数的学习,使学生掌握复变函数的基本知识和基本理论,了解它在自然科学等方面的一些应用。
2.在学习数学分析的基础上,将实函数和复变函数比较学习,从而使学生对分析学有更完整系统的认识和掌握。
3.通过对复变函数的学习,使学生对中学数学的有关内容如初等函数、代数基本定理等有更深的理解。
三、教学内容和要求
第一章 复数与复变函数
第一节 复数
1. 掌握复数的定义性质、复数的表示方法及复数的四则运算;
2.理解复数在几何中的应用。
第二节 复平面上的点集
1. 理解平面点集的几个概念、等价描述及相互关系;
2. 理解连续曲线、Jordan曲线、光滑曲线的概念、 Jordan定理和区域的定义。
第四节 复变函数
1理解复变函数、极限、连续、一致连续的定义及连续函数的性质;
2了解复变函数和实函数的区别与联系。
第四节 复球面与无穷远点
1. 了解什么是扩充复平面及无穷远点来源。
本章重点实掌握关于共轭复数的一些等式;关于模的等式与不等式;复数的不同表示形式并善于根据不同问题选用适当的表示;复数的乘、除、乘方、开方运算; 三点共线的条件,实数方程化成复数方程;充分理解入变换、满变换和一一变换;复函数极限的等价刻画;扩充复平面上一些性质及广义极限、广义连续.
第二章 解析函数
第一节 解析函数的概念与Cauchy-Riemann 条件
1. 理解解析函数的概念及性质,弄清解析、连续、可微的关系;
2.掌握判定函数解析的充要条件、充分条件和必要条件;
3.掌握判断一个函数是否可微或解析。
第二节 初等解析函数
1.掌握几个初等复函数的定义及性质;
3.理解函数在实数域和复数域的区别与联系。
第三节 初等多值函数
1.理解复函数具有多值性的原因;
2. 掌握应用限制幅角或割破平面来确定其单值解析分支;
3. 掌握利用一点来确定分支,然后求另外一点的值。
本章的重点是解析函数的刻画,熟练判定函数的解析性与可微性;熟练掌握几个初等函数的性质及与实函数的区别与连续;理解复函数产生多值的原因,确定单值解析分支的方法,掌握求多值函数在某一点的值.
第三章 复变函数的积分
第一节 复积分的概念及其简单性质
1.理解复积分的定义和基本性质,会利用定义和定理求复积分;
2.理解实积分和复积分的区别联系.
第二节 Cauchy积分定理
1.理解柯西积分定理及其几种推广的条件和结论;
2. 理解积分定理的证明思想;
3. 掌握运用柯西定理、柯西公式、高阶导数公式等求复积分。
第三节 Cauchy积分公式及其推论
1.掌握Cauchy积分公式及其证明;
2.掌握Cauchy不等式及Liouville定理、代数基本定理及其证明;
3.理解解析函数无穷阶可微的性质;
4.掌握Morera定理、证明及其简单应用。
第四节 解析函数与调和函数的关系
1.掌握调和函数的定义、调和函数与解析函数的关系;
2.掌握已知解析函数的实部(虚部)来求虚部(实部),从而可求得一个解析函数的方法。
第五节 平面向量场――解析函数的应用
1.了解平面向量场的几个概念。
本章的重点是在复积分的基础上对积分定理和积分公式的深刻理解和掌握;运用它们证明 Liouville定理、代数基本定理及Morera定理,并掌握这些定理的应用;掌握调和函数和解析函数的关系,掌握已知解析函数的实部(虚部)来求虚部(实部),从而可求得一个解析函数的方法。
第四章 解析函数的幂级数表示法
第一节 复级数的基本性质
1.理解复数项级数收敛性判定及几种收敛概念与相互关系,理解函数项级数一致收敛的性质;
2. 掌握Weierstrass定理。
第二节 幂级数
1.掌握幂级数收敛半径的求法即幂级数在收敛圆周上的了敛散性;
2.掌握幂级数和函数的解析性质。
第三节 解析函数的Taylor展式
1.理解Taylor定理及证明思想;
2.掌握幂级数的和函数在收敛圆周上的性质;
3.掌握求一些初等函数的Taylor展式的方法。
第四节 解析函数零点的孤立性及唯一性定理
1.掌握解析函数零点的判定方法;
2.掌握解析函数零点的孤立性定理、唯一性定理、最大(最小)模定理及它们的证明;
3.掌握解析函数零点的孤立性定理、唯一性定理、最大(最小)模定理的应用。
本章的主要内容是以级数理论为工具,研究解析函数的性质. 重点掌握Weierstrass定理、
解析函数零点的孤立性定理、唯一性定理、最大(最小)模定理及它们应用.
第五章 解析函数的Laurent展式
第一节 解析函数的Laurent展式
1.了解双边幂级数的概念及双边幂级数在收敛圆环内的性质;
2. 理解Laurent定理及证明思想,理解 Laurent 级数与Taylor级数的关系;
3. 掌握解析函数在孤立奇点邻域内的Laurent展开.
第二节 解析函数的孤立奇点
1. 掌握孤立奇点的分类与判定方法;
2. 理解本质奇点的性质,掌握Weierstrass定理,理解Picard定理;
3. 掌握Schwarz引理及其证明方法.
第三节 解析函数在无穷远点的性质
1. 理解无穷远点是孤立奇点的定义;
2. 理解无穷远点奇点类型的判定方法。
第四节 整函数与亚纯函数的概念
1. 理解亚纯函数的概念;
2. 掌握整函数的性质定理、函数为有理函数的充要条件。
第五节 平面向量场-解析函数的应用
1. 了解奇点在平面向量场中的应用。
第六章 残数理论及其应用
第一节 留数
1. 掌握留数的定义(包括有限点和无穷点),留数的求法;
2. 掌握留数定理及应用留数定理计算复积分;
3. 了解含无穷点区域的留数定理。
第二节 用残数定理计算实积分
1. 掌握应用留数定理计算四种实积分的方法;
2. 了解几种特殊实积分的计算及其意义。
第二节 辐角原理及其应用
1.掌握对数留数、辐角原理及其应用;
2.掌握Rouche 定理及其应用;
3.掌握单叶解析函数的性质。
本章的主要内容是有限点留数的概念和留数定理;有限奇点处留数的求法;无穷点处留数的概念和计算方法; 用留数定理计算实积分(包括积分路径上有奇点的广义积分);零点与极点个数定理;辐角原理及其应用;Rouche定理及其应用。
第七章 保形变换
第一节 解析变换的特性
1.掌握解析变换的性质(保域性、保角)
2. 理解单叶解析变换的共形性。
第二节 分式线性变换
1. 理解分式线性变换及其分解;
2. 理解分式线性变换的性质(共形性、保交比、保圆性、保对称点性);
3. 掌握分式线性变换的应用。
第三节 某些初等函数构成的保形变换
1. 掌握幂函数与根式函数,指数函数与对数函数的几何意义,并根据其求某些特殊的保形变换;
2.理解儒可夫斯基函数的单叶性区域。
第四节 关于保形变换的Riemann存在定理和边界对应定理
1. 理解Riemann存在与唯一性定理;
2. 了解和边界对应定理。
本章的主要内容是解析变换的保域性、保角性,单叶解析变换的保形性; 线性变换的性质及其应用;某些初等函数构成的保形变换及其作用;充分理Riemann 定义及其重要意义,充分了解别界对应定理.
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 复数与复变函数 |
3 |
2 |
|
|
1 |
|
|
|
第二章 解析函数 |
5 |
4 |
|
|
1 |
|
|
|
第三章 复变函数的积分 |
6 |
5 |
|
|
1 |
|
|
|
第四章 解析函数的幂级数表示法 |
5 |
4 |
|
|
1 |
|
|
|
第五章 解析函数的Laurent展式与孤立奇点 |
5 |
4 |
|
|
1 |
|
|
|
第六章 留数定理及其应用 |
5 |
4 |
|
|
1 |
|
|
|
第七章 共形映射 |
5 |
4 |
|
|
1 |
|
|
|
合 计 |
34 |
27 |
|
|
7 |
|
|
|
五、考核说明
本课程采用闭卷考试,成绩评定采用百分制,计算方法为期末总评成绩=期末考试成绩*70%+期中考试成绩*20%+平时成绩,其中平时成绩采取10分制,包括课堂表现和作业成绩。期末总评成绩不低于60分为及格。
六、主要教材及教学参考书目
(一)主要教材
1.钟玉泉 《复变函数论》(第三版) 高等教育出版社 2003年
(二)主要参考书目
1. 庄圻泰 张南岳 《复变函数》, 北京大学出版社,1984.
2. 普里瓦洛夫,《复变函数》,人民教育出版,1965 年
“统计学”教学大纲
教研室主任. 吕玉华 执笔人.温玉珍
一、课程基本信息
开课单位.澳门威斯尼斯615人官方
课程名称.统计学
课程编号.06202313
英文名称.Mathematical Statistics
课程类型.专业任选课
总 学 时. 34 理论学时. 34 实验学时. 0 课外学时.0
学 分. 2
开设专业.信息与计算科学
先修课程.数学分析(06200131)、高等代数(06200221)
二、课程任务目标
(一)课程任务
(本项编写要求.写明该课程的性质和任务)
统计学是概率论的后续课程,在现实中的应用性很强,是各种统计理论的数学基础分析理论,先期完成的课程必须有高等代数、数学分析、解析几何、概率论。
统计学是现代应用数学中一个有特色的分支;它在现代科学技术中占有很重要的地位,是研究自然现象,处理现代工程技术,解决科研和生产实际问题的有力武器之一,其方法已日益渗透到每一科学领域(包括自然科学、技术科学、社会科学、军事科学和管理科学)、工农业生产和经济管理部门。因此,本课程已成为统计学专业的主要专业课程之一。
本课程的主要内容有.抽样分布理论、估计理论、假设检验、回归分析和方差分析、统计决策以及Bayes统计。在教学过程中,应该注意理论联系实际,注意习题课程的讲授。
在本课程的执行过程中,内容的选取和讲解都考虑到了学生以后的发展。
(二)课程目标
(本项编写要求.写明学生在知识和能力方面应达到的目标要求)
在学完本课程之后,学生能够.
1.理解统计学的基本概念;
2.掌握参数估计的理论与方法、统计假设检验的主要方法、方差分析方法和回归分析方法,熟悉抽样分布理论,,以进一步掌握随机数学的思想方法和技巧;
3.掌握对受到随机性影响的数据进行收集、整理、建模、分析和推断的基本知识、基本理论和主要方法,为后继课程学习所需要的统计学知识打下基础,并为今后从事中等学校中有关统计学的教学工作打下基础;
三、教学内容和要求
(一)理论教学的内容及要求
(本项编写要求.以基本内容为主线,对各知识点分按“了解”、“理解”、“掌握”三个层次提出要求,并说明教学重点及难点)
第一章.抽样分布
第一节.基本概念
1. 理解总体、个体、简单随机样本的概念
2. 理解统计量的概念
3. 了解小样本问题、大样本问题
第二节.样本数字特征和分布
了解经验分布和格列纹科定理
掌握样本的数字特征,以及相关的计算
样本数字特征的分布
第三节.抽样分布定理
1.掌握抽样分布定理及其应用
第二章.估计理论
第一节. 矩法和极大似然法
1. 掌握矩法估计量以及计算
2. 掌握极大似然法估计量和有关的计算方法
第二节. 无偏性和优效性
1. 掌握无偏性以及基本性质和计算,会应用;
2. 掌握优效性的基本第一、理论和计算
3. 理解相合性的概念
第三节.区间估计
1.掌握区间估计的定义和计算
第三章.假设检验
第一节. 基本概念
1.了解假设检验的基本概念
第二节. 参数假设检验
1. 掌握期望的检验方法和计算
2. 方差的假设检验方法和相关计算
第三节. 非参数检验
1. 掌握分布函数的假设检验和计算
第四节. 最佳检验
1.区分两类错误,掌握其概念
2. 了解功效函数的定义和计算
3. 掌握最佳检验的方法和计算
第四章.回归分析和方差分析
第一节. 线性模型
1.了解模型的建立
第二节. 最小二乘法估计
1. 掌握参数最小二乘法估计的原理
2. 掌握参数最小二乘法估计的性质
第三节. 应用例题、曲线回归
理解例题的方法
了解曲线回归方法
第四节. 假设检验
1.掌握线性模型和回归系数的假设检验
第五节. 单因子方差分析
1.了解单因子方差分析
第五章.统计决策以及Bayes统计
第一节. 极大极小估计
1.掌握极大极小估计量的定义和计算方法
第二节. Bayes统计学
1. 了解Bayes估计的定义和性质,掌握计算方法
2. 掌握区间估计的定义和计算
3. 掌握假设检验的计算方法
第三节. 应用
1.了解统计决策以及Bayes统计的具体应用
注.打(*)号内容可由教师选择是否讲授。
四、学时分配
(本项编写要求.按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章.抽样分布 |
6 |
5 |
|
|
1 |
|
|
|
第二章.估计理论 |
7 |
6 |
|
|
1 |
|
|
|
第三章.假设检验 |
7 |
6 |
|
|
1 |
|
|
|
第四章.回归分析和方差分析 |
7 |
6 |
|
|
1 |
|
|
|
第五章.统计决策以及Bayes统计 |
7 |
6 |
|
|
1 |
|
|
|
合 计 |
34 |
29 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
课程考试考核方法.闭卷考试.
总评=期末考试为主(70%)+期中考试(20%)+平时作业为辅(10%)
六、主要教材及教学参考书目
(本项编写要求.写明教材及主要教学参考书目的编著者、书名、出版社、出版时间)
(一)主要教材
1.《概率论及数理统计》(下) 梁之舜等编 高等教育出版社(2005年2月第三版)。
(二)主要参考书目
1. 茆诗松等编 概率论及数理统计教程 高等教育出版社;
2. 陈家鼎等编 统数理统计学讲义 高等教育出版社
《数学物理方程》教学大纲
教研室主任:郑召文 执笔人:李傅山
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数学物理方程
课程编号:06202413
英文名称:Equations of Mathematical Physics
课程类型:专业任选课
总 学 时:34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算科学
先修课程:数学分析(06200131) 复变函数(062022131) 常微分方程(06200611)
二、课程任务目标
(一)课程任务
数学物理方程是一门重要的基础课程. 数学物理方程的目的就是用微积分的思想,结合线性代数,解析几何,普通物理学和常微分方程的知识,来解决数学理论本身和其它学科中出现的若干具有重要理论价值和应用价值的微分方程问题. 充分利用数学的方法进行抽象,从具体到抽象,从特殊到一般,而最后所得到的解或所证明的解的性质也要应用于具体的问题并同时经受检验。进而将所得到的结论与方法用于更大范围的现象和事物,起到举一反三的作用。
通过这门课的学习和训练,使学生学会和掌握偏微分方程的基础理论和方法,使学生们学习数学建模的一些基本方法,初步了解一些典型方程描述的物理现象,理解典型方程及定解问题的导出过程,掌握分离变量法、Fourier变换法、Green函数法等经典方法,并可熟练运用于有关定解问题的求解,为将来从事相关领域的科学研究工作培养兴趣,做好准备.
(二)课程目标
在学完本课程之后,学生能够:
1. 使学生学会和掌握偏微分方程的基础理论和方法,为他们学习其它数学理论及后续课程打下基础;
2. 通过这门课本身的学习和训练,使学生们学习数学建模的一些基本方法,初步了解一些典型方程描述的物理现象,理解典型方程及定解问题的导出过程,掌握分离变量法、Fourier变换法、Green函数法等经典方法,并可熟练运用于有关定解问题的求解,为将来从事相关领域的科学研究工作培养兴趣,做好准备.
三、教学内容和要求
(一)理论教学的内容及要求
第一章 波动方程
第一节 方程的导出、定解条件
1. 理解波动方程导出所应用的物理规律、导出过程和其所描述的物理现象;
2. 掌握三种定解条件的提出;
3. 理解定解问题适定概念及数学物理方程所研究的问题。
第二节 d’Alembert公式、波的传播
1. 理解叠加原理、齐次化原理的意义;
2. 掌握弦振动方程 Cauchy 问题的d’Alembert解法;
3. 掌握依赖区间、决定区域和影响区域;
4. 理解传播波。
第三节 初边值问题的变量分离法
1. 掌握初边值定解问题的变量分离方法(包括非齐次方程和非齐次边界条件的情形);
2. 理解解的物理意义。
第四节 高维波动方程的Cauchy问题
1. 理解膜振动方程的导出;
2. 掌握定解问题的提出;
3. 掌握球平均方法和降维法求解高维Cauchy问题。
第五节 波的传播与衰减
1. 掌握依赖区域、决定区域和影响区域;
2. 理解Huygens原理、波的弥散;
3. 掌握波动方程解的衰减性。
第六节 能量不等式、波动方程解的唯一性和稳定性
1. 掌握初边值问题解的唯一性与稳定性;
2. 掌握Cauchy问题解的唯一性与稳定性。
本章主要内容是数学模型的建立,初边值问题和Cauchy问题的解法,解的几何和物理意义,
解的唯一性和稳定性。 难点是高维波动方程Cauchy问题的解法,对高维方程的初边值问题只能解决特殊区域上的情形。
第二章 热传导方程
第一节 热传导方程及其定解问题的导出
1. 理解热传导方程导出所应用的物理规律、导出过程及描述的物理现象;
2. 掌握定解条件的提法,并注意和波动方程定解提法比较。
第二节 初边值问题的变量分离
1. 掌握一维热传导方程初边值问题的解法,并注意和波动方程的比较;
2. 理解圆形区域上初边值问题的解法。
第三节 Cauchy问题
1. 掌握Fourier变换的及其性质;
2. 掌握 一维Cauchy 问题的Fourier 解法及解的存在性验证.
第四节 极值原理、定解问题解的唯一性与稳定性
1.掌握极值原理及物理解释,并说明波动方程无极值原理;
2.掌握初边值解的唯一性与稳定性;
3.掌握Cauchy问题解的唯一性与稳定性.
第五节 解的渐近形态
1.掌握初边值问题解的渐近性态,并和波动方程比较;
2.掌握Cauchy问题解的渐近性态并和波动方程比较.
本章的主要内容是热传导模型的导出, 初边值问题和Cauchy问题的解法,解的唯一性与稳定性,解的渐近形态. 难点是Fourier变换解Cauchy问题和极值原理的证明. 再讲授热传导方程要注意和波动方程的比较, 波动方程无极值原理, 同时波动方程Cauchy问题的低维和高维问题差别很大, 而热传导方程 Cauchy问题低维和高维问题差别不显著, 热传导方程解的唯一性与稳定性也可以用能量估计方法解决.
第三章 调和方程
第一节 建立方程、定解条件
1. 理解方程的导出;
2. 掌握定解条件的提法;
3. 掌握变分原理思想及其重要作用.
第二节 Green 函数及其应用
1.掌握Green公式的各种表达形式;
2.掌握 Poisson方程解的表达公式、平均值原理和极值原理;
3.掌握应用极值原理证明Dirichlet边值问题解的唯一性与稳定性.
第三节 Green函数
1.掌握Green 函数的定义、性质, 掌握特殊区域上Green函数的表达式;
2.掌握特殊区域上调和方程解的表达公式的导出及解的验证;
3.掌握调和函数的性质.
第四节 强极值原理、第二边值问题解的唯一性
1.理解强极值原理;
2.掌握应用强极值原理证明第二边值问题解的唯一性;
3.掌握用能量积分方法证明解的唯一性并注意和波动方程和热传导方程的比较.
本章的主要内容是Poisson解的表达公式, Green 函数及其性质,特殊区域上调和方程解的表达公式, 调和函数的性质, 极值原理和强极值原理及解的唯一性与稳定性. 难点是应用Green函数求解调和方程定解问题, 调和函数的性质.
第四章 二阶线性偏微方程的分类和总结
第一节 二阶线性方程的分类
1.掌握两个自变量的二阶线性偏微分方程的分类和化简;
2.理解多个自变量方程的分类.
第二节 二阶线性方程的特征理论
1.理解特征概念;
2.掌握特征方程的导出并求某些方程的特征方程.
第三节 三类方程的比较
1.理解线性方程的叠加原理;
2.理解解的性质的比较及物理解释;
3.掌握定解问题的提法的比较.
第四节 先验估计
1. 掌握椭圆方程和热传导方程的比较原理及最大模估计;
2.掌握波动方程、热传导方程和椭圆方程的能量估计及其应用.
本章的主要内容是方程的分类和化简,方程的特征理论及应用;三类方程性质比较、
定解提法比较, 椭圆和热传导方程的最大模估计和三类方程的能量估计.难点是特征方程的导出和先验估计.
第五章 广义解和广义函数
第一节 广义解
1.理解研究广义解的必要性;
2.理解强解和弱解.
第二节 广义函数的概念
1.理解广义函数的物理背景和广义解的数学概念;
2.掌握基本函数空间和三类广义函数.
第三节 广义函数的性质与运算
1.掌握广义函数的极限、导数、乘子;
2.掌握广义函数的卷积.
第四节 广义函数的Fourier变换
1.理解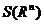 上的Fourier变换;
上的Fourier变换;
2.理解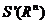 上的Fourier变换.
上的Fourier变换.
第五节 基本解
1.掌握波动方程和热传导方程Cauchy问题的基本解及其作用;
2.掌握调和方程的基本解;
3.理解其它类型的基本节.
本章的主要内容是广义函数及其性质与运算, 广义函数的Fourier变换, 基本解. 难点是广义函数的Fourier变换和基本解.
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:波动方程 |
6 |
5 |
|
|
1 |
|
|
|
第二章:热传导方程 |
7 |
6 |
|
|
1 |
|
|
|
第三章:调和方程 |
7 |
6 |
|
|
1 |
|
|
|
第四章:二阶PDE的分类和总结 |
7 |
6 |
|
|
1 |
|
|
|
第五章:广义解与广义函数 |
7 |
6 |
|
|
1 |
|
|
|
合 计 |
34 |
29 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用闭卷考试,成绩评定采用百分制,计算方法为期末总评成绩=期末考试成绩*70%+期中考试成绩*20%+平时成绩,其中平时成绩采取10分制,包括课堂表现和作业成绩。期末总评成绩不低于60分为及格。
六、主要教材及教学参考书目
(一)主要教材
1.谷超豪,李大潜等,《数学物理方程》第二版,高等教育出版社,2003年。
(二)主要参考书目
1. 姜礼尚 等, 数《数学物理方程讲义》,,高等教育出版社,1995年。
2.F John,Partial Differential Equations, Springer,1982年.
“组合优化”教学大纲
教研室主任:郑召文 执笔人:苗翠霞
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:组合优化
课程编号:06202513
英文名称:Combinatorics Mathematics
课程类型:专业任选课
总 学 时:34 理论学时:34 习题课时:0 课外学时:0
学 分:2
开设专业:信息与计算科学
先修课程:概率论(06200711)
二、课程任务目标
(一)课程任务
组合优化是计算机科学与技术专业本科专业选修课程之一, 它主要讲授排列组合原理、母函数与递推关系、容斥原理和鸽笼原理以及组合算法与复杂性分析,并能应用这些方法解决某些实际问题。
(二)课程目标
通过本课程的学习,要使学生具有现代数学的观点和方法,初步掌握常用组合计数的构造思想和计算方法。同时,也要培养学生抽象思维和慎密概括的能力,使学生具有良好的开拓专业理论的素质和使用所学知识,分析和解决实际问题的能力。
三、教学内容和要求
(一)理论教学的内容及要求
第1章 排列与组合
§1.1 基本计数法则
§1.3排列
§1.5 组合
§1.6 排列的生成算法
1.6.1 序数法
1.6.2 字典序法
1.6.3 换位法
§1.8 允许重复的组合
本章教学重点和难点
重点:运用排列与组合进行计数以及排列的生成算法。
难点:换位法和允许重复的组合。
本章教学基本要求
使学生掌握运用排列与组合进行计数;
第2章 母函数与递推关系
§2.1 母函数的引入
§2.2 母函数的性质
2.2.1 若干基本的母函数
2.2.2 基本公式
§2.3 整数的拆分
§2.6 指数型母函数
2.6.1 问题的提出
2.6.2指数型母函数的引入
§2.7 递推关系举例
本章教学重点和难点
重点:母函数的性质,整数的拆分和指数型母函数。
难点:指数型母函数。
本章教学基本要求
1. 使学生了解母函数的性质与递推关系;
2. 熟练掌握整数的拆分和指数型母函数。
第3章 容斥原理与鸽巢原理
§3.1 容斥原理
3.1.1 引论
3.1.2 容斥原理的两个基本公式
3.1.3 例子
§3.3 广义的容斥原理
3.3.1 问题的引入
3.3.2 特殊情况
3.3.3 一般公式
§3.4 广义的容斥原理的若干应用
§3.10 鸽巢原理
3.10.1 问题的引入
3.10.2 一般的鸽巢原理
§3.12 拉蒙赛(Ramsey)数
3.12.1拉蒙赛数问题
3.12.2拉蒙赛数
本章教学重点和难点
重点:容斥原理和鸽笼原理的应用。
难点:拉蒙赛(Ramsey)数。
本章教学基本要求
1.让学生熟练掌握容斥原理和鸽笼原理及其应用。
2.让学生学了解拉蒙赛(Ramsey)数。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第1章:排列与组合 |
10 |
8 |
|
|
2 |
|
|
|
第2章:母函数与递推关系 |
12 |
10 |
|
|
2 |
|
|
|
第3章:容斥原理与鸽巢原理 |
12 |
10 |
|
|
2 |
|
|
|
合 计 |
34 |
28 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、课程论文等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+课程论文成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.卢开澄 卢华明编《组合数学》(第3版), 清华大学出版社,2002年.
(二)主要参考书目
1.《组合数学》 胡端平, 鲁晓成 武汉大学出版社 2001年
2.《组合数学》 曹汝成 华南理工大学出版社 2005年
“C++语言程序设计”教学大纲
教研室主任:赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:C++语言程序设计
课程编号:06202713
英文名称:C++ language programming
课程类型:专业方向任选课
总 学 时: 34 理论学时:34 实验学时:0 课外学时:0
学 分: 2
开设专业:信息与计算专业
先修课程:C语言程序设计(17000210)
二、课程任务目标
(一)课程任务
C++语言程序设计是面向对象编程技术,本课程主要介绍C++语言基础知识,C++程序结构,函数,类与对象,数组、指针与字符串,继承与派生,多态性,群体类,群体数据的组织,流类库与输入/输出,异常处理,MFC库与Windows程序开发。
(二)课程目标
使学生掌握一门面向对象高级程序设计语言,了解面向对象程序设计方法,具有基本的程序设计的能力,为Windows下编程打好基础。
在学完本课程之后,学生能够:
掌握面向对象程序设计的基本概念与方法。
能够利用 C++ 语言解决一般应用问题。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 概述
1.了解计算机程序设计语言的发展;
2.掌握面向对象的方法;
3.掌握面向对象的软件开发;
4.掌握信息的表示与存储;
5.了解程序的开发过程。
第二章 C++ 简单程序设计
1.熟练掌握C++语言的数据类型与表达式;
2.熟练掌握数据的输入输出处理;
3.熟练掌握C++语言的基本控制结构;
4.熟练掌握自定义数据类型的应用;
5.学会分析、编写利用基本控制结构进行数据存储、输入输出处理的简单程序。
第三章 函数
1.熟练掌握函数的定义与使用;
2.熟练掌握函数重载和函数模板;
3.熟练掌握带默认形参值的函数的使用;
4.掌握内联函数和C++系统函数;
5.学会分析、编写利用函数进行数据处理的简单程序。
第四章 类与对象
1.熟练掌握抽象、封装、继承和多态的概念;
2.熟练掌握类的声明、成员函数、成员的访问控制、对象的概念;
3.熟练掌握构造函数和析构函数;
4.掌握类的组合、类模板和面向对象标记。
第五章 C++程序的结构
1.熟练掌握C++的作用域和可见性及二者的联系;
2.熟练掌握生存期、局部变量、全局变量、数据成员、静态成员等概念;
3.熟练掌握常引用、常对象和利用const修饰的类成员;
4.熟练掌握多文件结构和编译预处理命令;
5.掌握友元函数、友元类;
6.学会分析、编写符合C++程序结构的单文件和多文件程序。
第六章 数组、指针和字符串
1.熟练掌握一维数组的使用;
2.熟练掌握指针操作;
3.熟练掌握动态内存分配与释放的方法;
4.掌握多维数组的使用方法;
5.掌握字符串存储与处理的方法;
6.学会数组、指针、字符串和动态内存分配技术进行程序设计。
第七章 继承与派生
1.熟练掌握C++语言的继承与派生的方法;
2.熟练掌握访问控制;掌握派生类构造和析构函数;
3.掌握派生类的成员的标识与访问;
4.掌握赋值兼容规则;
5.学会利用C++语言的继承与派生理论,进行简单程序设计。
第八章 多态性
1.熟练掌握多态的概念和应用;
2.熟练掌握运算符重载;
3.掌握虚函数和抽象类的概念;
4.学会综合应用多态理论,编写简单程序。
第九章 群体类
1.掌握线性群体的概念;
2.掌握栈类、队列类、数组类、链表类的特点和简单应用;
3.了解C++标准库中的容器类的应用;
4.学会综合应用线性群体编写简单程序。
第十章 群体数据的组织
1.了解插入、选择、顺序、交换、折半排序的方法;
2.了解标准C++库中的简单算法实现方法。
第十一章 流类库与输入/输出
1.熟练掌握I/O流的概念;
2.熟练掌握输出流、输入流的构造、成员函数等的使用;
3.掌握有关输入/输出流的程序设计方法;
4.学会综合应用输入/输出流编写简单程序。
第十二章 异常处理
1.熟练掌握异常处理的基本思想流;
2.熟练掌握C++异常处理的语法、接口声明等的实现;
3.掌握异常处理中的构造与析构;
4.学会编写具有异常处理能力的简单程序。
第十三章 MFC库与Windows程序开发概述
1.了解Windows的编程模式和使用Visual C++开发Windows程序的步骤;
2.了解MFC库概念及应用。
1. 四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 概述 |
1 |
1 |
|
|
|
|
|
|
第二章 C++ 简单程序设计 |
1 |
1 |
|
|
|
|
|
|
第三章 函数 |
1 |
1 |
|
|
|
|
|
|
第四章 类与对象 |
8 |
8 |
|
|
|
|
|
|
第五章 C++程序的结构 |
2 |
2 |
|
|
|
|
|
|
第六章 数组、指针和字符串 |
1 |
1 |
|
|
|
|
|
|
第七章 继承与派生 |
6 |
6 |
|
|
|
|
|
|
第八章 多态性 |
2 |
2 |
|
|
|
|
|
|
第九章 群体类 |
2 |
2 |
|
|
|
|
|
|
第十章 群体数据的组织 |
2 |
2 |
|
|
|
|
|
|
第十一章 流类库与输入/输出 |
2 |
2 |
|
|
|
|
|
|
第十二章 异常处理 |
2 |
2 |
|
|
|
|
|
|
第十三章 MFC库与Windows程序开发概述 |
4 |
4 |
|
|
|
|
|
课程设计(自定) |
合计 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方法:考查
成绩评定的方法:总评成绩=期末考试(70%)+课程设计(20%)+平时与作业(10%)
最终成绩分为:优秀(90和90以上),良好(80至89),中等(70至79),及格(60至69),不及格(60以下)。
六、主要教材及教学参考书目
(一)主要教材
1. 郑莉等 编《C++语言程序设计》,清华大学出版社
(二)主要参考书目
1.郑莉等 编《C++语言程序设计习题与实验指导》,清华大学出版社
2.郑阿奇主编《Visual C++ 实用教程》(第2版),电子工业出版社,2003.8。
“汇编语言”教学大纲
教研室主任:赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:汇编语言
课程编号:06202913
英文名称:Assembler Language
课程类型:专业方向任选课
总 学 时: 34 理论学时:34 实验学 课外学时:
学 分:2
开设专业:信息与计算专业
先修课程:C语言程序设计(17000210)
二、课程任务目标
(一)课程任务
汇编语言是计算机能提供给用户的最快而又最有效的语言,也是能够利用计算机所有硬件特性直接控制硬件的唯一语言,因而在对于程序的空间和时间要求很高的场合,则更是非常用汇编语言不可了。本课程的基本任务是:使学生了解和掌握80x86计算机CPU的结构,存储器的组织方式,8086/8088计算机的寻址方式,8086/8088指令系统, 80x86、Pentium增强和扩充指令,基本的汇编语言程序设计方法和技能及高级汇编语言技术,并能熟练运用汇编语言进行程序设计。
(二)课程目标
汇编语言程序设计是计算机专业中一门十分重要的课程,通过本课程的学习,使学生掌握汇编语言的基本结构、基本指令、能用汇编语言进行简单的程序设计;了解汇编语言的强大功能;了解汇编语言与高级语言的接口等。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 基础知识
了解并掌握二进位计数制及不同基数的数之间的相互转换;
了解计算机中数和字符的表示和几种基本的逻辑运算。
第二章 80x86 计算机组织
1.了解计算机系统构成;
2.掌握80x86计算机CPU的结构;
3.掌握存储器的组织方式;
4.了解外部设备。
第三章80x86 的指令系统和寻址方式
1.掌握8086/8088计算机的寻址方式;
2.掌握8086/8088指令系统;
3.了解80x86、Pentium增强和扩充指令;
4.了解DOS系统功能调用。
第四章 汇编语言程序格式
1. 理解汇编程序功能;
2. 掌握伪操作及汇编语言程序格式;
3. 熟悉汇编语言的上机过程。
第五章 循环与分支程序设计
1.掌握循环程序设计的原理及相关程序设计方法;
2.掌握分支程序设计的原理及相关程序设计方法。
第六章 子程序结构
掌握子程序的设计方法;
理解子程序的嵌套;
了解递归子程序。
第七章 高级汇编语言技术
了解宏指令及其相关程序设计方法。
第八章 输入/输出程序设计
1.理解I/O设备的数据传送方式;
2.了解程序直接控制I/O方式;
3.了解中断传送方式。
第九章 BIOS和DOS中断
1.了解BIOS中断的功能;
2.了解DOS中断的功能;
3.掌握常用的中断功能。
第十章 单色和彩色图形显示
1.了解INT10设置显示方式的方法;
2.了解单色和彩色图形显示的异同;
第十一章 发声系统的程序设计
1.理解发声系统的工作原理
2.掌握发声系统的程序设计的方法。
第十二章 磁盘文件存取技术
1.了解磁盘文件存取方式;
2.了解顺序文件与随机文件的读取方法。
第十三章 模块化程序设计
了解汇编语言的强大功能。
(二)实践教学的内容及要求
(上机时间学生自我安排)
1.DEBUG 的启动及其基本命令的使用
了解DEBUG 的命令,掌握基本的DEBUG指令。
2.DEBUG编程
熟悉DEBUG命令,用DEBUG命令执行机器指令,理解8086的机器指令。
3.汇编语言程序格式
熟悉汇编语言程序格式,熟悉汇编语言的上机过程。
4.循环与分支程序设计与子程序设计
掌握汇编语言程序格式,掌握汇编语言的上机过程,掌握子程序的格式。
5.输入/输出程序设计与中断
了解中断服务程序的结构,理解中断向量的提取与置入方法。
6.发声系统的程序设计
理解发声系统的工作原理,了解汇编语言的强大功能。
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 基础知识 |
1 |
1 |
|
|
|
|
|
|
第二章 80x86 计算机组织 |
2 |
2 |
|
|
|
|
|
|
第三章80x86 的指令系统和寻址方式 |
12 |
12 |
|
|
|
|
|
|
第四章 汇编语言程序格式 |
1 |
1 |
|
|
|
|
|
|
第五章 循环与分支程序设计 |
3 |
3 |
|
|
|
|
|
|
第六章 子程序结构 |
4 |
4 |
|
|
|
|
|
|
第七章 高级汇编语言技术 |
1 |
1 |
|
|
|
|
|
|
第八章 输入/输出程序设计 |
3 |
3 |
|
|
|
|
|
|
第九章 BIOS和DOS中断 |
1 |
1 |
|
|
|
|
|
|
第十章 单色和彩色图形显示 |
1 |
1 |
|
|
|
|
|
|
第十一章 发声系统的程序设计 |
3 |
3 |
|
|
|
|
|
课程设计(自定) |
第十二章 磁盘文件存取技术 |
1 |
1 |
|
|
|
|
|
|
第十三章 模块化程序设计 |
1 |
1 |
|
|
|
|
|
|
合计 |
34 |
34 |
|
|
|
|
|
|
五、考核说明
考核方法:考查
成绩评定的方法:总评成绩=期末考试(70%)+课程设计(20%)+平时与作业(10%)
最终成绩分为:优秀(90和90以上),良好(80至89),中等(70至79),及格(60至69),不及格(60以下)。
六、主要教材及教学参考书目
(一)主要教材
1.沈美明等 ,IBM PC汇编语言程序设计,清华大学出版社,2002
(二)主要参考书目
1.杨季文等编著 ,80X86汇编语言程序设计教程,清华大学出版社,2002
2.徐建民等编著,汇编语言程序设计,电子工业出版社,2001
“泛函分析”教学大纲
教研室主任:张克梅 执笔人:栾世霞
一、课程基本信息
开课单位:数学与信息科学学院
课程名称:泛函分析
课程编号:0623013
英文名称:Functional Analysis
课程类型:专业基础课
总 学 时:34 理论学时: 34 实验学时: 0 课外学时:0
学 分:2
开设专业:信息与计算数学
先修课程:数学分析(06200131)、实变函数(06202113)
二、课程任务目标
(一)课程任务
《泛函分析》课程是高等院校信息与计算数学专业本科生的一门重要的专业课程。它是现代教学中的一门较新的数学分支,它综合运用分析、代数、几何的观点和方法研究分析数学中的许多问题。泛函分析的基本概念、定理和方法已渗透到诸如:微分方程、概率论、理论物理、现代力学等信息与计算数学及其他学科的许多分支。本课程作为数学分析和实变函数课程的深化,具有承上启下的作用,是现代数学最重要的入门课程。它一方面为后继课程提供所需的理论基础,同时还为培养学生的抽象思维能力、逻辑推理能力和独立工作能力提供必要的训练。
(二)课程目标
在学完本课程之后,学生能够了解和掌握度量空间、赋范线性空间、Banach空间、内积空间、Hilbert空间、有界线性算子和泛函的基本概念和基本理论。通过对这门课程的教学培养学生的理论思维能力,为进一步学习数学的有关学科打下扎实的理论基础,同时对把它应用到数理经济、现代控制、量子场论、统计物理、工程技术等领域有很大帮助。
三、教学内容和要求
第一章 距离空间·赋范线性空间
第一节 距离空间的定义及例
1.了解距离空间的定义和几个常见的距离空间
2.掌握距离空间中的收敛概念及完备距离空间的概念
第二节 赋范线性空间是定义及例
1.掌握赋范线性空间、Banach空间的概念
2.了解常见的赋范线性空间
第三节 距离空间中的若干概念·连续映射
1. 了解并掌握距离空间中的一些基本概念,特别是邻域、开集、闭集、有界集、稠密集
2. 掌握判定集合稠密的充要条件
3. 掌握连续映射的概念及其判定
第四节 压缩映射原理及应用
1. 掌握并会应用压缩映射压缩映射原理
第五节 距离空间的完备化
1. 了解距离空间的完备化过程
2. 掌握完备距离空间的两个性质
第六节 可分距离空间
1. 掌握距离空间可分的定义
2. 了解几个常见的可分和不可分的距离空间
第七节 距离空间中几何的列紧性
1.理解掌握紧集的概念和判定
2.了解两个具体空间中集合列紧性的判定
第八节 关于赋范线性空间的若干概念
1.了解赋范线性空间的集合和映射的一些基本概念
2. 掌握范数等价的概念
第九节 有限维赋范线性空间的特征
1.掌握并会应用有限维赋范线性空间的特征
第二章 线性算子
第一节 线性算子的基本性质
1. 掌握有界线性算子的概念及其范数的概念
2. 掌握有界线性算子的性质及判定
3. 了解几个常见的有界线性算子
第二节 有界线性算子空间
1.了解有界线性算子空间的概念,掌握该空间的完备性
2.了解有界线性算子的各种运算,掌握并会应用逆运算
3.掌握有界线性算子的概念和性质
第三节 共鸣定理及其应用
1. 掌握共鸣定理内容并会证明
2. 掌握有界线性算子强收敛的充要条件
3. 了解共鸣定理的应用
第四节 开映射定理与逆算子定理·闭图像定理
1.掌握定理内容并会证明
2.了解乘积赋范空间的概念,掌握闭图像的概念
第三章 线性泛函
第一节 线性泛函的基本性质
1. 掌握线性泛函和有界线性泛函的基本性质
第二节 有界线性泛函的延拓
1. 了解Zorn引理
2. 了解实线性空间上线性泛函的延拓
3. 掌握有界线性泛函的保范延拓
第三节 某些空间上有界线性泛函的表示
1.掌握有限维空间上线性泛函的表示
2.了解某些具体空间上有界线性泛函的表示
第四节 共轭算子
1. 掌握共轭算子的概念和性质
2. 了解常见的共轭算子
第五节 弱﹡收敛与弱收敛·自反空间
1.了解自然嵌入映射,掌握自反空间的定义
2.掌握弱﹡收敛与弱收敛,并会应用
第四章 全连续线性算子
第一节 全连续算子的定义和性质
1. 掌握全连续线性算子的定义
2. 熟知全连续线性算子的性质
第二节 全连续算子方程的Riesz--schauder理论
1. 掌握Banach空间中全连续线性算子的Fredholm选择定理
2. 了解定理证明方法
第三节 全连续线性算子的谱
1.掌握有界线性算子谱的概念
2.掌握全连续算子谱的性质
第五章 Hilbert空间上的有界线性算子
第一节 Hilbert空间
1. 掌握内积空间和Hilbert空间的概念,熟知内积空间的特征
2. 掌握Hilbert空间的直交分解,会证明并应用变分引理
3. 掌握就范直交系和完备就范直交系的概念
4. 掌握并会应用Bessel不等式和Parseval等式
5. 了解无穷维的、可分的Hilbert空间的同构性质
第二节 Riesz表示定理
1. 理解掌握Hilbert空间上有界线性泛函的Riesz表示定理
第三节 自共轭算子的谱
1.掌握Hilbert空间中自共轭算子的概念与性质
2.理解Hilbert空间中自共轭算子的范数概念
3.熟练掌握自共轭算子谱的特征
第四节 自共轭全连续算子的谱分解
1. 掌握自共轭全连续算子谱的特征
2. 理解自共轭全连续算子的谱分解
第五节 投影算子
1.熟练掌握投影算子的概念与性质
第六节 非负算子
1. 掌握非负算子的概念
2. 了解非负算子的性质
第七节 自共轭算子的谱分解
1.了解全连续自共轭算子的谱分解
2.理解自共轭算子的谱分解定理
3.了解自共轭算子函数及其在研究算子谱的性质中的应用
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:距离空间·赋范线性空间 |
5 |
4 |
|
|
1 |
|
|
|
第二章:线性算子 |
8 |
6 |
|
|
2 |
|
|
|
第三章:线性泛函 |
7 |
6 |
|
|
1 |
|
|
|
第四章:全连续线性算子 |
7 |
5 |
|
|
2 |
|
|
|
第五章:Hilbert空间上的线性算子 |
7 |
6 |
|
|
1 |
|
|
|
合 计 |
34 |
27 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方法: 闭卷
成绩评定: 平时成绩30%(作业10%、期中考试20%);期末考试70%
六、主要教材及教学参考书目
(一)主要教材
1.郭大钧等《实变函数与泛函分析》下册,山东大学出版社,2004年。
(二)主要参考书目
1.程其襄等 《实变函数与泛函分析基础,高等教育出版社,2003年。
2. 王声望、郑维行 《实变函数与泛函分析概要》第二册,高等教育出版社,1994年。
“计算机维护与维修”教学大纲
教研室主任:赵京东 执笔人:叶传秀
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:计算机维护与维修
课程编号:06203113
英文名称:Maintenance of Computer
课程类型:专业任选课
总 学 时:34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算科学
先修课程:操作系统(06201512)
二、课程任务目标
(一)课程任务
计算机维护与维修是计算机相关各专业必修的一门专业基础课,也可作为非计算机专业的选修课。本书主要讲述了微机系统概论、微机的最新发展、最新的装机方法、微机常见故障分析与处理方法、常见主机故障处理、微机外设的维护与维修、微机的运行环境及保养、微机系统的设置与测试、微机操作系统的安装与设置、Windows操作系统常见故障处理、注册表的基本知识及使用技巧、计算机常见病毒的检测与防治、Windows下的Internet的配置与使用等内容。通过对本课的系统学习,使学生对计算机的各个部件有感性的认识并理性理解各个部件的功能和特点,学习微机出现故障时解决和处理的方法,为今后从事计算机应用和使用计算机提供必要的微机硬件知识,以便能够得心应手地使用好和维护好计算机,更好地使计算机发挥作用。其主要任务是为所学人员奠定计算机硬件的理论知识,培养实际动手能力,提高分析计算机软硬件问题。
(二)课程目标
在学完本课程之后,学生能够:
1. 使学生对计算机的各个部件有感性的认识并理性理解各个部件的功能和特点;
2. 能够为微机出现的故障提供解决和处理的方法;
3. 掌握计算机软硬件的知识,提高学生发现问题、解决问题的能力;
三、教学内容和要求
(一)理论教学的内容及要求
第一章 微机系统概论
第一节 微机硬件的系统结构
1.了解微机及微机硬件的发展概况;
2.掌握微机系统的组成和硬件结构;
3.理解微机的工作原理;
第二节 微机的基本配置
1.掌握微机的基本配置;
2.了解微机的可选配件和软件配置;
第三节 微处理器及其发展
1.了解微处理器的发展历史;
2.理解微处理器的内部结构;
3.了解Pentium微处理器、AMD微处理器;
4.了解微处理器的发展趋势;
第四节 存储器
1了解内存储器、高速缓存、外存储器、显示存储器的特点、功能和存储原理;
2了解内存储器、高速缓存、外存储器、显示存储器的主要产品;
第五节 总线技术
1.了解内部总线和外设总线结构和工作原理;
第六节 主板
1.了解主板的芯片组的主要厂商;
2. 了解主板的CPU接口类型;
3.了解主板的物理结构标准;
4.掌握BIOS、CMOS芯片的功能;
5.了解BIOS的工作原理和主要品牌;
6.了解总线扩展插槽、二级高速缓存、I/O接口和超频技术;
第七节 微机的选购与安装
1.掌握机箱及电源、主板、CPU、内存条、硬盘、光驱、软驱、显卡、显示器、键盘、鼠标等硬件的选购方法;
2.掌握计算机各构成部件的正确安装方法;
3.了解计算机的发展趋势;
本章教学重点:
1.计算机系统的系统结构及各构成部件的功能;
2.计算机各构成部件的选购与组装;
本章教学难点:
计算机系统各构成部件的工作原理;
第二章 微机的运行环境及维护方法
第一节 微机的运行环境
1.了解机房布局和环境要求;
2.了解机房的供电要求和接地系统;
第二节 微机的日常维护和管理
1.掌握计算机系统的常规性维护方法;
2.了解计算机运行环境的日常管理方法;
第三节 微机常见故障分析和维护方法
1.了解微机故障种类;
2.掌握微机故障的分析与判断、维修方法;
本章教学重点:
1. 计算机系统的常规性维护方法
2.微机故障的分析与判断、维修方法
本章教学难点:
微机故障的分析与判断、维修方法;
第三章 常见主机故障处理
第一节 主板及主板故障处理
1.了解主板类型与基本结构;
2.掌握主板的故障检测的方法;
3.掌握主板常见故障的处理的方法;
4.掌握主板BIOS刷新技术;
第二节 内存及内存故障处理
1.掌握内存类型;
2.了解内存的主要性能参数;
3.掌握内存故障处理的方法;
第三节 CPU常见故障处理
1.理解CPU的主要性能参数;
2.掌握CPU常见故障处理的方法、预防CPU烧毁的方法;
本章教学重点
1.主板、内存、CPU的故障处理方法;
2. 主板、内存、CPU的功能与参数指标;
本章教学难点
主板、内存、CPU的故障处理方法;
第四章 微机外设维护与维修
第一节 键盘和鼠标
1.了解键盘和键盘接口;
2.掌握键盘的维护与维修的方法;
3.了解鼠标的工作原理;
4.掌握鼠标的维护与维修的方法;
第二节 软盘和硬盘
1.了解磁盘驱动器、硬盘驱动器的基本结构;
2.理解软盘、硬盘的参数、性能指标和工作原理;
3.掌握软盘、硬盘故障的诊断与维修方法;
第三节 显示器和显卡
1.了解显示器、显卡的技术指标和工作原理;
2.掌握显示器、显卡故障的诊断与维修方法;
第四节 打印机
1.了解针式、激光、喷墨打印机的工作原理;
2.掌握打印机故障的排除方法;
本章教学重点:
外设故障的诊断与维修方法;
本章教学难点:
外设的工作原理与故障诊断;
第五章 多媒体计算机外设的维护与维修
第一节 光驱
1.了解CD-ROM的工作原理、性能指标;
2.掌握CD-ROM的安装方法和常见故障的解决方法;
第二节 声卡
1.了解声卡的工作原理和组成;
2.掌握声卡故障的诊断与排除方法;
第三节 视频卡
1.了解的视频卡的工作原理;
2.掌握视频卡的安装、故障诊断与排除方法;
第四节 扫描仪
1.了解扫描仪的工作原理及分类;
2.掌握扫描仪的维护的维护方法;
第五节 数码照相机
1.了解数码相机的工作原理及其主要部件;
2.掌握数码相机的安装和维护方法;
本章教学重点:
多媒体计算机外设的故障诊断与维修方法;
本章教学难点:
各多媒体外设的工作原理与故障诊断;
第六章 微机系统的设置与测试
第一节 BIOS与CMOS入门述
1.了解BIOS和CMOS的工作原理;
第二节 BIOS的基本功能
1.掌握BIOS的基本功能;
第三节 BIOS SETUP
1.掌握BIOS的设置方法;
第四节 COMS菜单项设置
1.掌握CMOS的设置方法;
2.掌握CMOS中的信息保存与恢复方法;
第五节 加电故障定位与维修测试工具
1.了解常用测试工具软件的使用方法;
第六节微机CMOS参数设置的优化
1.掌握CMOS参数设置的优化方法;
2.掌握BIOS应用技巧及故障处理方法;
第七节 AWARD公司BIOS的升级方法
1.了解AWARD主板;
2.理解AWARD主板升级方法;
第八节CBROM的使用方法简介
1.了解CBROM具体使用法;
2.了解主板加入还原卡功能的方法
本章教学重点:
BIOS与CMOS的设置与测试方法;
本章教学难点:
BIOS设置与升级;
第七章 操作系统的安装与设置
第一节 操作系统的发展
1.了解操作系统的发展历程;
2.了解操作系统的种类;
第二节 软硬盘的组织结构
1.了解软硬盘的组织结构;
第三节 DOS与Windows 98 的安装与设置
1.掌握DOS、Windows98系统的安装与设置方法;
2.了解Dos、Windows98系统的系统要求;
第四节 其他操作系统
1.掌握Windows2000、Windows xp系统的安装与设置方法;
2.掌握Unix系统的安装与设置方法;
本章教学重点:
各类操作系统的安装与设置方法;
本章教学难点:
Windows xp与Unix操作系统的安装与设置;
第八章 常见故障实例
第一节 硬件故障
1.掌握硬件故障的判断方法;
2. 掌握常见的硬件故障处理方法;
第二节 Windows 98/Me故障处理
1.了解Windows 98/Me常见的安装故障与引导故障;
2.掌握Windows 98/Me故障的处理方法;
第三节 多媒体故障处理
1.了解多媒体故障的原因;
2.掌握多媒体故障的处理方法;
第四节 处理
1.了解网络故障的原因;
2.掌握网络故障的处理方法;
第五节 其他故障处理
1.了解其他故障的诊断与处理方法;
本章教学重点:
各种常见故障的诊断与处理方法;
本章教学难点:
各种常见故障的诊断与处理方法;
第九章 注册表
第一节 注册表的概念
1.了解注册表的打开方式与功能;
第二节 注册表的结构
1.了解注册表的结构特点;
第三节 注册表的主键
1.了解注册表的主键;
第四节 注册表的使用技巧
1.掌握注册表的备份与恢复方法;
2.掌握注册表编辑器的使用方法;
本章教学重点:
1.注册表的备份与恢复;
2.注册表的使用技巧;
本章教学难点:
注册表的使用技巧;
第十章 计算机病毒的检测与防治
第一节 计算机病毒的产生和分类
1.了解计算机病毒的定义、分类、特点;
第二节 计算机病毒的预防
1.了解计算机病毒的构成、传染的基本条件及方式;
2.掌握计算机病毒的预防、防治和清除的方法;
本章教学重点:
计算机病毒的预防、防治和清除的方法;
本章教学难点:
计算机病毒的预防、防治和清除的方法;
第十一章 设置与使用Internet
第一节 认识Internet
1.了解Internet提供的信息服务的连接方式;
第二节 Modem的安装与配置
1.掌握内置Modem与外置Modem安装的方法;
2.掌握Modem故障的处理方法;
第三节 其他的接入方式
1.了解ISDN、ADSL的工作原理;
第四节 Internet基本设置
1.掌握 Internet基本设置的方法;
2.了解常见的故障及其处理方法;
第五节 常用WWW浏览器运用
1.了解WWW浏览器的使用方法;
(二)实践教学的内容及要求
1. 实验一:在DOS系统下进行分区 FDISK和格式化FORMAT,并使硬盘能引导DOS系统,安装Window系统和显卡、主板驱动程序。
掌握安装操作系统、进行硬盘分区和格式化、Windows 下安装显卡驱动程序、主板驱动程序的方法;掌握安装过程中出现问题的诊断与处理方法;
2. 实验二:硬盘实用程序、GHOST、PQ、DM的使用。
了解硬盘的特点,掌握硬盘克隆软件Ghost、分区工具PQmagic、和硬盘管理程序DM软件的使用方法;
3.实验三:电脑组装。
了解计算机的硬件组成及各部件的选型;掌握电脑的组装流程和正确的安装方法;
4.实验四:计算机系统优化。
了解注册表的使用方法和系统的状态;掌握计算机系统的优化方法和常用优化软件的使用方法;
5.实验五:故障诊断与处理
了解常见的故障分类;掌握常见故障的诊断方法与故障处理方法;
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:微机系统概论 |
2 |
2 |
|
|
|
|
|
|
第二章:微机的运行环境及维护方法 |
2 |
2 |
|
|
|
|
|
|
第三章:常见主机故障处理 |
6 |
6 |
|
|
|
|
|
|
第四章:微机外设维护与维修 |
4 |
4 |
|
|
|
|
|
|
第五章:多媒体计算机外设的维护与维修 |
2 |
2 |
|
|
|
|
|
|
第六章:微机系统的设置与测试 |
4 |
4 |
|
|
|
|
|
|
第七章:操作系统的安装与设置 |
3 |
3 |
|
|
|
|
|
|
第八章:常见故障实例 |
3 |
3 |
|
|
|
|
|
|
第九章:注册表 |
3 |
3 |
|
|
|
|
|
|
第十章:计算机病毒的检测与防治 |
3 |
3 |
|
|
|
|
|
|
第十一章:设置与使用Internet |
2 |
2 |
|
|
|
|
|
|
合 计 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方式:闭卷;
总评成绩=期中成绩×0.2+平时(包括作业、上机实验考核,总分为10分)+期末成绩×0.7
六、主要教材及教学参考书目
(一)主要教材
1.查志琴等著《计算机维护与维修》第2版 电子工业出版社 2003年8月
(二)主要参考书目
1.查志琴等著《计算机维护与维修》第2版 电子工业出版社 2003年8月
2.曹然彬,武传宝著,《计算机维护与维修》,清华大学出版社,2006年9月
“数学实验”教学大纲
教研室主任: 赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:数学实验
课程编号:06203213
英文名称:Mathematical Experiment
课程类型:专业任选课
总 学 时:34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算数学
先修课程:数学分析(06200131) 高等代数(06200221)
二、课程任务目标
(一)课程任务
本课程是一门数学类专业学科基础课课程。本课程的任务是使学生掌握数学实验的基本思想和方法,即不把数学看成先验的逻辑体系,而是把它视为一门“实验科学”,从问题出发,通过学习Mathematica数学软件,借助计算机,学生亲自设计和动手,体验解决问题的过程,从实验中去学习、探索和发现数学的规律。
(二)课程目标
在学完本课程之后,学生能够:
1. 熟悉Mathematica数学软件的安装、启动、退出;
2. 熟悉计算机基本操作,掌握Mathematica语言程序的设计与编写,能编程解决一些数学问题;
3. 能独立地进行实验前预习准备,会书写实验报告。
三、教学内容和要求
(一)理论教学的内容及要求
第一部分 Mathematica简介
Mathematica中的基本量
了解Mathematica中的基本量:数、变量、表、初等函数、自定义函数、表达式等的定义及运算。
第二节 在Mathematica中作图
掌握Plot, ParametricPlot, Plot3D, ParametricPlot3D, ListPlot函数以及图形元素作图函数Point, Line, Circle,Polygon等的用法。
第三节 初等代数运算
掌握多项式运算、方程求根、和与积等函数的用法。
第四节 微积分
了解求极限、求微商与微分、求定积分与不定积分、幂级数展开、求解微分方程等函数。
第五节 线性代数
掌握向量和矩阵的定义与运算、方程组求解等函数。
第六节 数值计算方法
掌握Interpolation, Fit, FindRoot, NIntegerate, FindMinimum等函数的用法。
第七节 过程编程
熟练掌握几种条件控制结构和循环控制结构。
第二部分 有关实验
实验一 微积分基础
1. 掌握借助Mathematica图形功能研究函数的性质的方法;
2. 了解编制对数表的方法;
3. 了解调和级数与欧拉常数的关系;
4. 掌握画双曲正弦(余弦)曲线的方法;
5. 了解双曲函数名称的由来。
实验二 怎样计算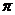
掌握用数值积分法、泰勒级数法、蒙特卡罗法计算 及其它未知量的方法。
及其它未知量的方法。
实验三 最佳分数近似值
了解怎样用分母小、误差小的分数近似值逼近实数及连分数理论。
实验四 数列与级数
掌握用图象研究数列极限行为的方法。
实验五 素数
1. 掌握探索素数有无穷多个的方法;
2. 学会用筛法和试除法构造素数表;
3. 了解探索素数生成公式的有关工作;
4. 了解素数的分布规律。
实验六 概率
1. 掌握用随机模拟法求事件概率的方法;
2. 了解二项分布,普阿松分布,正态分布的有关知识。
实验七 几何变换
了解各种变换(线性变换、射影变换、非欧几何变换、复变换等)下平面图形的变化情况及不变量。
实验八 天体运动
1. 通过计算机模拟了解产生天体运动、电场作用等物理现象;
2. 掌握微分方程的数值解等数学方法。
实验九 迭代(一)----方程求解
1. 掌握用迭代方法求解方程和方程组的方法;
2. 了解影响收敛速度的各种因素。
实验十 寻优
了解均匀搜索法,0.618法,求导法,最速下降法,最小二乘法。
实验十一 最速降线
了解寻找最速降线、等时曲线的思想方法。
实验十二 迭代(二)----分形
1. 了解生成元的概念;
2. 了解Koch曲线,Hilbert曲线, Sierpinski三角形的生成方法;
3. 了解IFS迭代的思想。
实验十三 迭代(三) ----混沌
了解混沌现象及其所蕴涵的规律性。
实验十四 密码
1. 了解单表密码、多表密码、现代序列密码体制的主要缺陷;
2. 掌握 RSA公钥体制的原理和方法。
(二)实践教学的内容及要求
1. Mathematica编程及实现
熟练掌握Mathematica的各种函数及格式,掌握Mathematica编程及实现。
2. 教材中的有关实验
从教材中选取6~7个实验,相关要求参见理论教学的内容及要求。
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一部分:Mathematica简介 |
17 |
15 |
|
|
2 |
|
|
|
第二部分:有关实验 |
17 |
15 |
|
|
2 |
|
|
|
合 计 |
34 |
30 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合。期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+期中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.李尚志等《数学实验》,高等教育出版社,2004年。
(二)主要参考书目
1.乐经良等《数学实验》,高等教育出版社,1999年。
2.萧树铁等《数学实验》,高等教育出版社,1999年。
“计算机原理”教学大纲
教研室主任:赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:计算机原理
课程编号:06203413
英文名称:The Principles of Micro Computer
课程类型:专业任选课
总 学 时: 34 理论学时:34 实验学时: 课外学时:
学 分:2
开设专业:信息与计算科学
先修课程:C语言程序设计(17000210),计算机文化基础(17000110)
二、课程任务目标
(一)课程任务
计算机原理是理工科学生学习和掌握计算机硬件知识和汇编语言程序设计的入门课程。通过本课程的学习,使学生从应用的角度出发,在理论和实践的上掌握微机的基本组成、工作原理、汇编语言程序设计、接口电路及硬件的连接。建立系统的整体概念,使学生具有微机应用系统软、硬件相结合开发的初步能力。
(二)课程目标
本课程围绕微型计算机原理和应用主题,以Intelx86CPU为主线,系统介绍微型计算机的基本知识、基本组成、体系结构和工作模式等;Intelx86CPU的指令系统、汇编语言及程序设计方法和技巧;存储器的组成和I/O接口扩展方法;微机的中断结构、工作过程和8259A的编程与应用;微机中的常用接口原理和应用技术,包括串并行接口8255A和8251A的工作原理及编程应用方法,计数器/定时器8253的结构和应用,A/D、D/A的基本工作原理及应用方法。从而使学生能较清楚的了解微机的结构与工作流程,建立起系统的概念,初步掌握微机应用系统软、硬件开发技术。
课程在此基础上,对现代微机系统中涉及的总线技术、高速缓存技术、数据传输方法、高性能计算机的体系结构和主要技术作了简要分析。
同时,配以适当的实验教学培养学生的独立分析问题和解决问题的能力,通过系统的实践教学锻炼,使学生具有一定的软硬件开发能力,为未来的工作和后继课程的学习打下基础。
三、教学内容和要求
(一)理论教学的内容及要求
(本项编写要求:以基本内容为主线,对各知识点分按“了解”、“理解”、“掌握”三个层次提出要求,并说明教学重点及难点)
第一章 微型计算基础知识
第一节 微机基本结构
1.了解微机基本结构;
2.了解微机的主要性能指标。
第二节 计算机中的数制和编码
1.掌握10、2、8、16进制数之间的相互转换;
2.掌握机器数的表示方法;
3.掌握常用的字符编码;
第三节 基本数字逻辑电路
1.掌握基本逻辑电路;
2.掌握基本的逻辑代数;
3.掌握二进制运算;
第二章 80X86微处理器结构
第一节 80X86微处理器系列概况
1.了解80X86微处理器的发展过程;
第二节 8086微处理器
1.熟悉8086微处理器的内部结构、外部引脚;
2.掌握8086微处理器的内部寄存器;
3.熟悉8086微处理器访问存储器的持性、输入与输出组织;
第三节 8086微计算机组成
1.理解最小模式下的典型配置;
2.理解最大模式下的典型配置;
3.掌握总线周期。
第四节 先进微处理机介绍
1.了解80386、80486、奔腾(Pentium)微处理器的新增功能
第三章 IBM PC的指令系统与汇编语言
第一节 IBM PC的寻址方式
1.掌握与数据有关的寻址方式
2.掌握与转移地址有关的寻址方式
第二节 用DEBUG运行汇编语言程序
第三节 IBM PC的指令系统
1.掌握数据传送指令
2.掌握算术指令
3.掌握逻辑指令
4.掌握串处理指令
5.掌握控制转移指令
6.了解处理机控制指令
第四节 汇编语言程序的格式
1.掌握汇编程序的功能
2.掌握汇编语言程序格式
3.掌握汇编语言子程序
4.掌握汇编语言编程举例
第四章 存储器系统
第一节 存储器的分类与性能指标
1.掌握存储器的分类
2.了解存储器的主要性能指标
第二节 存储器的单元结构
1.了解RAM基本单元电路
2.了解纯ROM基本单元电路
第三节 存储器的基本结构
1.掌握存储体阵列
2.掌握地址译码驱动电路
3.熟悉数据I/O电路
4.掌握读写控制逻辑
第四节 微型计算机内存的通常结构
1.掌握存储容量扩展
2.了解多模块结构的存储器系统扩展
第五节 存储器应用举例
1.掌握SRAM应用
2.掌握动态RAM应用
3.掌握只读存储器(ROM)应用
第六节 外存储器简介
1.了解硬盘及硬盘驱动器
2.了解软盘及软盘驱动器
3.了解光盘
第五章 中断技术与DMA
第一节 中断技术概述
第二节 80X86的中断结构
1.掌握中断类型
2.掌握中断优先权
3.了解中断管理
第三节 微机系统的中断处理过程
1.理解中断请求
2.掌握中断响应的过程
3.掌握中断处理的过程
4.掌握中断返回的过程
第四节 8259A中断控制器
1.了解一般中断控制器的功能
2.掌握可编程中断控制器8259A工作特点
3.掌握259A的外部引脚信号
4.掌握8259A的工作原理
5.掌握8259A的编程结构
6.了解中断管理方式
7.掌握8259A的初始化流程
8.学会应用8259A
第五节 DMA控制器8237A
1.了解DMA的基本操作过程
2.了解8237A的编程结构和外部连接
3.掌握8237A的工作模式和模式寄存器的格式
4.掌握8237A控制寄存器的格式
5.掌握状态寄存器的格式
6.掌握请求标志和屏蔽标志的设置
7.掌握复位命令和清除先/后触发器命令
8.掌握8237A的初始化编程
第六章 接口技术及应用
第一节 接口的功能及在系统中的连接
1.了解接口的功能
2.了解接口与系统的连接
第二节 串行通信与8251A可编程串行口控制器
1.掌握串行通信的特点、串行通信的物理标准
2.掌握8251A的基本性能
3.掌握8251A的基本工作原理
4.掌握8251A的编程
第三节 8253计数器/定时器
1.了解可编程计数器/定时器的工作原理
2.掌握可编程计数器/定时器8253
3.掌握8253的应用
第四节 8255A可编程并行接口
1.了解8255A的结构和功能
2.了解8255A的引脚信号
3.掌握8255A的控制字
4.掌握8255A的工作方式说明
第五节 模/数和数/模转换
1.了解数/模(D/A)转换器
2.了解模/数(A/D)转换器
第六节 键盘与显示
1.掌握键盘设计
2.掌握LED数字显示电路的设计
(二)实践教学的内容及要求
(上机时间学生自我安排)
1.IBM PC的指令系统与汇编语言
了解8086的指令系统,掌握指令系统的各种寻址方式,理解常用指令的功能,掌握汇编言语的格式。
2.中断技术
理解中断的概念和中断的功能,掌握中断向量表,掌握中断向量的提取与置入方法,学会中断服务程序的编写格式。
3.8251A可编程串行口控制器
掌握8251A初始化步骤,了解串行口控制器的工作过程,掌握串行口通迅的编程方法。
4.8253计数器/定时器
掌握8253初始化步骤,了解计数器/定时器的工作过程,掌握计数器/定时器的编程方法。
5.键盘与LED数字显示电路的设计
掌握键盘与LED数字显示电路的设计步骤,了解键盘与LED数字显示电路的设计的工作原理,掌握键盘与LED数字显示电路的设计的编程方法。
6.综合应用
掌握键盘、LED、8253计数器/定时器电路的设计步骤,掌握多模块电路设计的编程方法。
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 微型计算基础知识 |
1 |
1 |
|
|
|
|
|
|
第二章 80X86微处理器结构 |
3 |
3 |
|
|
|
|
|
|
第三章 IBM PC的指令系统与汇编语言 |
16 |
16 |
|
|
|
|
|
|
第四章 存储器系统 |
2 |
2 |
|
|
|
|
|
|
第五章 中断技术与DMA |
2 |
2 |
|
|
|
|
|
|
第六章 接口技术及应用 |
10 |
10 |
|
|
|
|
|
课程设计(自定) |
合 计 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方法:考查
成绩评定的方法:总评成绩=期末考试(70%)+课程设计(20%)+平时与作业(10%)
最终成绩分为:优秀(90和90以上),良好(80至89),中等(70至79),及格(60至69),不及格(60以下)。
六、主要教材及教学参考书目
(一)主要教材
1. 赵京东等编著《微机原理与接口技术》,中国铁道出版社,2006年。
(二)主要参考书目
1.戴梅萼 编著《微型计算机技术及应用》,清华大学出版社,1991
2. 钱晓捷 陈涛编著 《16/32位微机原理、汇编语言及接口技术》,机械工业出版社,2001
“应用随机过程”教学大纲
教研室主任:吕玉华 执笔人:董华
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:应用随机过程
课程编号:06203513
英文名称:Applied Stochastic Processes
课程类型:学科基础课
总 学 时: 34 理论学时:34 实验学时: 0 课外学时:0
学 分:2
开设专业:信息与计算科学
先修课程:概率论(0620711)
二、课程任务目标
(一)课程任务
通过随机过程课程的学习,使学生掌握随机过程的基本概念。针对专业特点和专业要求,力求以概率的观点来讲述随机过程的理论,逐步培养学生利用随机过程的理论和技能解决应用概率问题。培养学生运用随机过程的方法分析问题、解决问题的能力。通过随机过程的整个教学过程,不断提高学生素质,为培养我国社会主义现代化建设的高层次、综合型人才作准备。
(二)课程目标
在学完本课程之后,学生能够:
1.对随机现象有充分的感性认识和比较准确的理解;
2.可以以概率的观点来讲述随机过程的理论,能够利用随机过程的理论和技能解决应用概率问题;
三、教学内容和要求
(一)理论教学的内容及要求
第一章 预备知识
第一节 概率空间
1、了解概率空间的三个元素;掌握s代数和可测空间、测度空间的定义。熟练运用概率的基本性质。
2、了解和掌握集合的上极限和下极限的含义。
第二节 随机变量和分布函数
1、掌握单个随机变量的密度函数、分布函数的含义及特点。
2、掌握多个随机变量的联合密度函数、联合分布函数的意义及求法。掌握示性变量在计数过程或计数变量中的意义及常用技巧。
第三节 数字特征、矩母函数与特征函数
1、掌握随机变量的期望、方差及协方差的含义及求法。了解常见随机变量的统计特征,掌握条件期望的求法。
2、了解Riemann-Stieltjes 积分的定义。注意区别Riemann-Stieltjes 积分与Riemann 积分的区别与联系。
3、了解测度积分的定义的步骤,掌握测度积分的基本性质,熟练使用测度积分的单调收敛定理、Fatou 引理、Lebesgue 控制收敛定理。
4、掌握矩母函数、特征函数及拉普拉斯变换的定义和各自的优缺点,了解常用概率分布的矩母函数。
第四 节条件概率、条件期望和独立性
1、掌握条件概率的定义,熟练使用全概率公式和Bayes 公式计算事件的概率。
2、掌握条件期望的定义和熟练使用性质。
3、了解独立性的含义,包括随机变量的独立性,事件族的独立性,s代数的独立性。掌握Borel-Cantelli 引理的条件和结论。掌握独立随机变量和的分布。
第五节 收敛性
1、了解几乎处处收敛、依概率收敛、和p 阶收敛的含义和相互关系。
第二章 随机过程的基本概念和基本类型
第一节 基本概念
1、了解随机过程的样本路径的含义。
第二节 有限维分布可Kolmogorov 定理
1、了解随机过程的有限维分布的含义和性质,掌握过程均值函数、协方差函数的定义。
2、了解Kolmogorov 定理及其理论意义。
第三节 随机过程的基本类型
1、了解平稳过程、协方差平稳过程和弱平稳过程的含义及区别。了解均值遍历性定理、协方差遍历性定理的条件和结论。
2、掌握随机过程中独立增量和平稳增量的意义及性质。
第三章 泊松过程
第一节 泊松过程
1、了解计数过程,掌握计数过程中独立增量和平稳增量的含义。
2、了解泊松过程,理解泊松过程的两个等价定义。
第二节与Poisson 过程相联系的若干分布
1、了解泊松过程中事件的来到间隔序列的定义, 掌握齐次泊松过程的来到间隔序列为独立同分布的指数随机变量,进而理解齐次泊松过程的无记忆性。
2、掌握齐次泊松过程中等待时间随机变量的定义、概率密度函数、常数强度函数。在了解顺序统计量的基础上,掌握齐次泊松过程中来到时刻的条件分布,掌握利用条件分布解决排队系统中与忙期有关的问题的方法。
第三节 Poisson 过程的推广
1、掌握非平稳或非齐次泊松过程的定义、强度函数。理解当强度函数有界时,可以将非齐次泊松过程看作一个齐次泊松过程的随机取样。
2、掌握复合泊松过程的定义,理解泊松过程(非齐次泊松过程)与复合泊松过程的关系及本质区别。
3、掌握条件泊松过程的定义, 在理解条件泊松过程不具有独立增量的基础上了解条件泊松过程并不是一个泊松过程。
第四章 更新过程
第一节 更新过程的定义及若干分布
1、了解更新过程实质上是一种计数过程,而泊松过程又是一种特殊的更新过程,理解在有限时间内不可能有无限多次更新发生。
2、进一步熟悉计数过程与等待时间的概率关系,掌握更新函数的表达式及有限性。
第二节 更新方程
1、了解利用更新过程中的极限定理来证明长时间后更新发生的速率等于更新的平均速度的期望,了解瓦尔德等式。
第三节 更新定理
1、掌握基本更新定理及其证明过程, 并能熟练地将基本更新定理运用于常见概率分布随机变量。
2、掌握格点的概念,了解布莱克威尔定理。
3、掌握关键更新定理,了解布莱克威尔定理与关键更新定理的等价性。理解剩余寿命与年龄的极限分布是相同的这一结论。掌握极限平均剩余寿命的概念及求解方法。
第四节 更新过程的推广
1、掌握延迟更新过程及相关极限定理。
2、掌握交错更新过程及其在年龄和剩余寿命等问题中的应用。
3、了解更新酬劳过程及其在剩余寿命问题中的应用。
第五章 马尔可夫链
第一节 基本概念
1、掌握马尔可夫链和马尔可夫性的定义,掌握马尔可夫链的特征及条件,能熟练写出常见Markov 链转移概率矩阵。了解切普曼-柯尔莫哥洛夫方程。
第二节 状态分类及性质
1、掌握马尔可夫链中相通、类、周期、常返、瞬态、正常返等概念,熟悉赌博模型的相关性质。了解马尔可夫链中类之间的转移,掌握赌徒输光模型中类之间的概率转移问题。
第三节 极限定理及平稳分布
1、掌握马尔可夫链的极限定理,能够利用马尔可夫链的极限定理解决排队问题、更新过程年龄问题。
2、掌握马尔可夫链中不变分布、极限分布的概念。能够利用不变分布求解markov 的极限分布。
第四节 马尔可夫链的应用
1、了解分支过程,掌握从单个个体开始群体迟早灭绝的概率的求解方法。
2、了解人口结构变化的Markov 链模型
3、了解Markov 链在数据压缩中应用。
第五节 连续时间马尔可夫链
1、掌握连续时间马尔可夫链的定义、性质、及其与离散时间马尔可夫链的区别,了解构造连续时间马尔可夫链的方法,熟悉连续时间马尔可夫链中瞬时状态、吸收状态、规则等概念,掌握转移速率的概念及其与离散时间马尔可夫链中转移速度的区别。
2、了解生灭过程,了解纯生过程及其与一般生灭过程的关系,了解尤尔过程及其与一般生灭过程的关系,掌握尤尔过程在时刻t 的群体总量给定时出生时刻的条件分布。
第六节 转移概率 和柯尔莫哥洛夫微分方程
和柯尔莫哥洛夫微分方程
1、掌握Q 矩阵的概念。了解柯尔莫哥洛夫向前和向后微分方程,了解柯尔莫哥洛夫微分方程与柯尔莫哥洛夫方程的关系, 熟练掌握求解连续时间马尔可夫链问题的转移矩阵的方法。
第六章 鞅
第一节基本概念
1、掌握上鞅、下鞅和鞅的概念。掌握随机游动模型中鞅的性质。掌握条件Jensen 不等式。熟练掌握条件期望的概念和基本性质
第二节 鞅的停时定理及一个应用
1、掌握停时的概念。了解几种常见的停时。掌握停时的性质。
2、掌握停时定理的含义。熟练运用停时定理来解决赌徒模型中的问题。
3、了解期权的含义。了解停时定理在计算期权值的界的具体过程。掌握停时定理的方法。
第三节 一致可积性
1、掌握一致可积性的含义和判别条件。掌握一致可积鞅的性质和停时定理。
第四 鞅收敛定理
1、和掌握鞅的收敛性定理。掌握一致收敛性与鞅收敛定理的关系。熟练使用鞅的收敛定理来解决分枝过程、随机游动以及Polya 模型的问题。
第五节 连续鞅
1、连续鞅的含义和性质。了解连续鞅的停时定理、鞅收敛定理。了解鞅在Lunderberg-Cramer 破产模型中的作用。
第七章 布朗运动
第一节 基本概念与性质
1、了解布朗运动的来由和本质,了解布朗运动与随机游动的区别与联系。掌握布朗运动过程的定义和独立增量性,掌握将一般布朗运动转化为标准布朗运动的方法。掌握独立增量的密度函数、联合密度函数和条件密度函数。
2、了解布朗运动路径的性质。了解布朗运动在[0.t]二次变差为t。
第二节、高斯过程
1、理解高斯过程并掌握高斯过程的定义,熟练使用独立增量性求Brown 运动的分布。
第三节 布朗运动的鞅性
1、掌握布朗运动的鞅的性质。
第四节 布朗运动的马尔可夫性
1、掌握连续Markov 过程的定义,熟悉布朗运动的马氏性和转移概率和转移密度。了解布朗运动的时间齐次性和空间齐次性的含义。
第五节 布朗运动的最大值变量和反正弦率
1、掌握布朗运动过程的击中时概念,掌握击中时随机变量的概率函数,了解击中时随机变量以概率1 为有限,而有无穷期望的性质。掌握布朗运动过程的最大值概念,掌握最大值随机变量的概率函数及其与击中时随机变量的概率函数的关系。
2、掌握起始点为x 的布朗运动在区间(a,b)的有零点的概率。了解布朗运动在时刻t 之前最后一个零点以及t 之后第一个零点的分布情况。
第六节 布朗运动的几种变化
1、了解布朗桥的含义及其在研究经验分布函数时的作用。
2、了解布朗运动的四种变化:1)在一个值处被吸收的布朗运动,2)在原点反射的布朗运动,3)几何布朗运动,4)积分布朗运动。掌握在一个值处被吸收的布朗运动的概率函数,掌握在原点反射的布朗运动及几何布朗运动的分布函数、期望和方差,掌握积分布朗运动的本质、期望和协方差。
3、了解有漂移的布朗运动的来由,掌握将有漂移的布朗运动转化为标准布朗运动的方法,熟悉有漂移的布朗运动的击中时随机变量和最大值随机变量
第八章 随机积分
第一节 关于随机游动的积分
1、了解关于随机机游动的积分的概念。
第二节 关于布朗运动的积分
1.掌握关于布朗运动的积分定义及性质。
2、掌握一些常见的布朗运动的积分的方法。
第三节 伊藤积分过程
1.掌握伊藤积分过程的定义及性质,掌握伊藤积分过程的二次变差及二次协变差的计算。
第四节 伊藤公式
1.掌握伊藤公式及其应用。
第五节 布莱克-斯克尔斯模型
1、了解布莱克-斯克尔斯模型及布莱克-斯克尔斯方程。
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:准备知识 |
2 |
2 |
|
|
|
|
|
|
第二章:随机过程的基本概念和基本类型 |
2 |
2 |
|
|
|
|
|
|
第三章:泊松过程 |
5 |
4 |
|
|
1 |
|
|
|
第四章:更新过程 |
5 |
4 |
|
|
1 |
|
|
|
第五章:马尔可夫链 |
5 |
4 |
|
|
1 |
|
|
|
第六章:鞅 |
5 |
4 |
|
|
1 |
|
|
|
第七章:布朗运动 |
5 |
4 |
|
|
1 |
|
|
|
第八章 随机积分 |
5 |
4 |
|
|
1 |
|
|
|
合 计 |
34 |
28 |
|
|
6 |
|
|
|
五、考核说明
课程考试考核方法:闭卷考试:
总评=期末考试为主(70%)+期中考试(20%)+平时作业为辅(10%)
六、主要教材及教学参考书目
(本项编写要求:写明教材及主要教学参考书目的编著者、书名、出版社、出版时间)
(一)主要教材
1、《应用随机过程》,张波著,中国人民大学出版社,2001;
(二)主要参考书目
1、《随机过程》,(美)S. M. 劳斯著,何声武等译,中国统计出版社,1997年。
2、《随机点过程及其应用》,邓永录著,科学出版社。1999 年
“图形与图像处理”教学大纲
教研室主任: 赵京东 执笔人:赵京东
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:图形与图像处理
课程编号:06203713
英文名称:Graphics & Image processing
课程类型:专业任选课
总 学 时: 34 理论学时:34 实验学时: 课外学时:
学 分:2
开设专业:信息与计算专业
先修课程:C语言程序设计(17000210),计算机文化基础(17000110)
二、课程任务目标
(一)课程任务
用计算机进行数学图形图像处理是当前计算机应用中十分活跃的领域,它将计算机的强大计算功能应用到矩阵运算,并通过大量的数学运算对图像进行变换、增强、复原、编码、与压缩等。本课程主要任务是利所学过的高等数学知识,通过Maglab语言进行数字图形绘制,对数字图像进行变换、增强、复原、编码与压缩等,为进一步深造打下基础。
(二)课程目标
掌握Maglab语言的基本语法和常见函数,了解M文件与M函数的关系,了解对象句柄的含义,了解图像的类型和格式,掌握图像类型之间的转换函数,理解图像的正交变换,理解滤波器的设计与应用,理解图像变换、增强、复原、编码、与压缩等函数。
三、教学内容和要求
(一)理论教学的内容及要求
第一章 MATLAB基础
1.了解MATLAB的特点;
2.掌握MATLAB的工作界面;
3.掌握MATLAB的基本语法;
4.掌握MATLAB的基本函数;
5.掌握MATLAB的M文件
第二章 MATLAB图形绘制基础
1.掌握数基本绘图函数与图形窗口的修饰;
2.掌握plot3函数;
第三章 MATLAB图形对象
1.理解图形对象;
2.掌握视频信息获取技术及实时处理技术句柄图形对象结构树;
3.掌握Image, Axes, Line, Rectangle, Surface, Light, Text对象;
4.了解Image, Axes, Line, Rectangle, Surface, Light, Text对象的属性。
第四章 MATLAB图形对象操作
1.了解图形对象的属性
2.了解图形对象句柄的获取函数
3.了解图形对象句柄的删除与判断
4.了解图形对象属性的获取与设置
第五章 GUI设计
1.了解GUI环境
2.了解GUI的设计原则
3.了解GUI的实现过程
第六章 MATLAB特殊图形的绘制
1.了解区域图、填充图、条形图、直方图、圆体图、饼图、排列图、离散图、散点图、轮廓图和向量图。
第七章 MATLAB高级绘图功能
1. 了解慧星图;
2. 了解帧动画与程序动画;
3. 了解色图变幻;
4. 了解voronoi图和三角剖分;
5. 了解四面体图、彩带图、伪彩图、切片图、网格图和曲面图等;
第八章 数字图像原理
1.了解图像文件格
2.掌握图像类型(索引图像、灰度图像、RGB图像、二值图像);
2.掌握图像类型转换的转换函数;
4.掌握图像数据类型转换的转换函数
第九章 图像显示与色彩
1.掌握imshow函数的格式与应用;
2.掌握colorbar函数的格式与应用;
3.理解RGB,NTSC,YCbCr和HSV颜色模型之间的关系及它们之间的转换函数。
第十章 图像正交变换
1. 理解傅里叶变换的特性;
2. 理解余弦变换的特性;
3. 掌握余弦变换函数;
4. 了解Walsh-Hadarnard变换,Radon变换,小波变换。
第十一章 滤波器的设计
1. 掌握imshow函数的格式与应用;
2. 掌握colorbar函数的格式与应用;
3. 理解RGB,NTSC,YCbCr和HSV颜色模型之间的关系及它们之间的转换函数。
第十二章 图像运算与区域处理
1. 掌握图像的点运算;
2. 掌握图像的算术运算;
3. 掌握图像的逻辑运算;
4. 理解图像的几何运算;
5. 了解图像的空间变换;
第十三章 图像增强
1. 掌握图像的灰度变换增强;
2. 了解图像的直方图灰度变换;
3. 了解空域滤波增强;
4. 了解频域增强;
5. 了解色彩增强;
6. 了解小波增强;
第十四章 图像复原
1. 理解图像的退化模型(连续退化模型、离散退化模型);
2. 了解图像复原的代数方法;
第十五章 图像分析
1. 了解图像的边缘检测(微分算子、拉普拉斯算子、Canny算子、四叉树分解);
第十六章 数学形态学操作
1. 理解数学形态学的基本运算(膨胀、腐蚀、开运算、闭运算);
第十七章 图像编码与压缩
1. 理解图像编码与压缩的意义;
2. 了解图像编码压缩的分类;
3. 了解图像编码压缩的评价;
4. 了解无损压缩编码的原理;
5. 了解有损压缩编码的原理;
(二)实践教学的内容及要求
(上机时间学生自我安排)
1.MATLAB6.5基础
掌握MATLAB6.5的安装;熟悉MATLAB6.5的工作界面;学会基本的数据输入与输出;
2.MATLAB图形绘制
掌握二维、三维图形的绘图方法及常见函数的应用。
3.GUI设计
掌握GUI的设计界面、常用控件;理解CALLBACK函数的功能。
4.特殊图形的绘制
了解区域图、填充图、条形图、直方图、圆体图、饼图、排列图、离散图、散点图、轮廓图和向量图的绘制方法。
5.imshow函数
掌握imshow函数的格式与应用;掌握colorbar函数的格式与应用;理解RGB,NTSC,YCbCr和HSV颜色模型之间的关系及它们之间的转换函数。
6.数字图像处理
掌握图像类型(索引图像、灰度图像、RGB图像、二值图像);掌握图像类型转换的转换函数;掌握图像数据类型转换的转换函数。
7.图像处理综合应用
理解图像增强、图像复原、图像编码与压缩。
四、学时分配
(本项编写要求:按章节简要编写各教学环节的学时分配)
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章 MATLAB基础 |
2 |
2 |
|
|
|
|
|
|
第二章 MATLAB图形绘制基础 |
4 |
4 |
|
|
|
|
|
|
第三章 MATLAB图形对象 |
2 |
2 |
|
|
|
|
|
|
第四章 MATLAB图形对象操作 |
2 |
2 |
|
|
|
|
|
|
第五章 GUI设计 |
2 |
2 |
|
|
|
|
|
|
第六章 MATLAB特殊图形的绘制 |
4 |
4 |
|
|
|
|
|
|
第七章 MATLAB高级绘图功能 |
1 |
1 |
|
|
|
|
|
|
第八章 数字图像原理 |
2 |
2 |
|
|
|
|
|
|
第九章 图像显示与色彩 |
2 |
2 |
|
|
|
|
|
|
第十章 图像正交变换 |
1 |
1 |
|
|
|
|
|
|
第十一章 滤波器的设计 |
1 |
1 |
|
|
|
|
|
|
第十二章 图像运算与区域处理 |
2 |
2 |
|
|
|
|
|
|
第十三章 图像增强 |
2 |
2 |
|
|
|
|
|
|
第十四章 图像复原 |
2 |
2 |
|
|
|
|
|
|
第十五章 图像分析 |
|
2 |
|
|
|
|
|
|
第十六章 数学形态学操作 |
1 |
1 |
|
|
|
|
|
|
第十七章 图像编码与压缩 |
2 |
2 |
|
|
|
|
|
课程设计(自定) |
合 计 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
考核方法:考查
成绩评定的方法:总评成绩=期末考试(70%)+课程设计(20%)+平时与作业(10%)
最终成绩分为:优秀(90和90以上),良好(80至89),中等(70至79),及格(60至69),不及格(60以下)。
六、主要教材及教学参考书目
(一)主要教材
1. 王家文等 编著《MATLAB6.5图形图像处理》,国防工为出版社,2004年。
(二)主要参考书目
1. 张志涌等 编著《精通MATLAB6.5》,北京航空航天大学出版社,2003年。
2. 刘维 编著,《精通MATLAB6.5与C/C++混合程序设计》,北京航空航天大学出版社,2004年。
“抽象代数”教学大纲
教研室主任:王培合 执笔人:孙宝芝
一、课程基本信息
开课单位:澳门威斯尼斯615人官方
课程名称:抽象代数
课程编号: 06203913
英文名称:Abstract Algebra
课程类型:专业基础课
总 学 时: 34 理论学时:34 实验学时:0 课外学时:0
学 分:2
开设专业:信息与计算数学
先修课程:高等代数(06200221)
二、课程任务目标
(一)课程任务
本课程主要任务是传授给学生代数思想方法及群、环、域的基本知识。《抽象代数》是数学专业基础课《高等代数》的后继课,它为学生继续学习与研究代数提供了足够的基础知识并充分展示了代数学的思维特点。通过本课程的学习,应使学生掌握群、环、域等基本概念、性质及一些经典结论,最重要的是,使学生能够灵活运用代数学思维方法和技巧。
(二)课程目标
在学完本课程之后,学生能够:
1. 对抽象代数的思想和方法有较深刻的认识,抽象思维、逻辑推理和运算的能力有所提高;
2. 获得一定的抽象代数的基础知识, 受到代数方法的初步训练, 为进一步学习代数后继课程打下基础;
3. 能应用抽象代数的知识与方法去理解与处理有关的问题, 培养与提高应用抽象代数的理论分析问题与解决问题的能力
三、教学内容和要求
(一)理论教学的内容及要求
第一章 群
第一节 等价关系与集合的分类
1了解商集的概念;
2理解等价关系与集合的分类的定义;
3掌握二者之间的关系;
第二节 群的概念;
1了解代数运算和群的一些例子;
2理解群的定义与群中单位元、可逆元的意义;
3掌握群的等价定义;
第三节 子群;
1了解子群的定义以及子群的运算性质;
2理解子群的等价定义和生成子群的构成;
3掌握子群的判断方法。
第四节. 群的同构;
1了解对称群的定义;
2理解群同构的定义和凯莱定理;
3掌握判断两个群同构的方法。
第五节; 循环群
1了解循环群以及生成元的定义:
2理解群中元素阶的定义;
3掌握循环群的子群与结构定理。
第六节. 置换群与对称群
1了解特殊n阶置换的定义;
2理解 n次对称群的定义与排列的关系;
3掌握把任意n阶置换表示成特殊置换的方法。
第七节 置换在对称变换群中的应用(本节为选学内容)
1了解对称变换群的定义;
2理解二面体群的定义;
3掌握某些对称变换群的求法。
第二章 群的进一步讨论
子群的陪集
1了解群中子集运算的性质和子群指数的定义,
2理解左右陪集的定义与性质以及;拉格朗日定理的内容;
3掌握拉格朗日定理在有限群分类中的应用。
正规子群与商群
1了解群的正规子群和单群的定义;
2理解正规子群的等价定义和商群的定义方法;
3掌握正规子群的判别方法。
群的同态和同态基本定理
1了解几个群同态的例子;
2理解群同态的定义与相关性质;
3掌握群同态基本定理并用之判断群之间的关系。
第四节 群的直积
1了解卡氏积的定义;
2理解群的内外直积的定义;
3掌握内外直积的性质与关系。
第五节群在集合上的作用
1了解特殊的群作用和稳定子;
2理解群作用的定义和不动元的定义;
3掌握有限群的类方程及其应用。
第六节. 西罗定理
1了解P群和的定义Sylow P子群的定义;
2理解P群和的定义Sylow P子群的定义;
3掌握掌握 Sylow 定理,并利用Sylow定理判断有限群的正规子群的情况。
第三章 环
第一节. 环的定义与基本性质
1了解特殊环以及单位元可逆元的定义;
2理解环和子环的定义,环与群之间的关系;
3掌握环中元素的运算性质和子环的判定
第二节 整环 域与除环
1了解环中零因子的概念和四元数体的构造;
2理解除环和域的定义;
3掌握整环定义和除环域的判别方法。
第三节 理想与商环
1了解特殊环中理想子环的构成;
2理解理想子环主理想子环的定义与元素形式以及商环的定义;
3掌握主理想子环的判别方法和商环的性质。
第四节 素理想与极大理想
1了解几类特殊环的素理想和极大理想;
2理解素理想和极大理想的关系;
3掌握素理想与极大理想的判别方法和关系。
环的同态
1了解几类特殊的环同态;
2理解环同态的定义以及与群同态的关系‘
3掌握环同态基本定理以及其与群同态基本定理的关系。
第六节. 环的特征与素域
1了解几类特殊环的特征;
2理解环的特征数的定义以及与加群中元素阶的关系;
3掌握整环以及域的特征数;
第四章 环的进一步讨论
第一节 多项式环
1了解未定元和形式幂级数环的定义;
2理解多项式环的定义和多项式的次数;
3掌握环与其上一元多项式环的关系。
第二节 整环的商域
1了解交换的无零因子环与域的关系;
2理解整环商域的构成和环的扩张定理的应用;
3掌握比较简单的整环的商域的求法。
第三节 唯一分解整环
1了解整环元素整除的定义了解单位、相伴元、真因子、素元 不可约元的定义以及之间的关系;
2理解唯一分解环的定义和性质;
3掌握唯一分解整环的判别方法;
第四节 主理想整环与欧几里得整环
1了解欧几里得算法;
2理解主理想整环、欧氏环的定义;
3掌握与主理想整环、欧氏环唯一分解整环相关的定理。
第五节 唯一分解整环上的多项式环
1了解本原多项式的概念;
2理解本原多项式的性质;
3掌握整环上的多项式环和其商域上多项式环的关系。
第五章 域的扩张
第一节 向量空间
1了解域上向量空间的分类;
2理解域上向量空间的定义子空间以及元素线性相关和无关的定义;
3掌握向量空间基的求法和维数的不变性。
第二节 扩域
1了解域论基本定理;
2理解扩域和单扩张的定义;
3掌握某些域的单扩域的构造。
第三节 多项式的分裂域
1了解多项式分裂域的存在性;
2理解分裂域的定义和同构意义下的唯一性;
3掌握一些特定多项式分裂域的求法。
第四节 代数扩张
1了解代数元和超越元的定义;
2理解最小多项式 有限扩张 无限扩张以及本原元的定义;
3掌握代数扩张的次数及其性质。
第五节 有限域
1了解有限域阶的性质;
2 理解有限域的唯一性和主要性质;
3掌握有限域的子域构成以及与有限循环群的子群构造相比较。
(二)实践教学的内容及要求(无)
四、学时分配
章 次 |
各教学环节学时分配 |
小计 |
讲授 |
实验 |
上机 |
习题 |
讨论 |
课外 |
备 注 |
第一章:群 |
6 |
5 |
|
|
1 |
|
|
|
第二章:群的进一步讨论 |
7 |
6 |
|
|
1 |
|
|
|
第三章:环 |
7 |
6 |
|
|
1 |
|
|
|
第四章:环的进一步讨论 |
7 |
6 |
|
|
1 |
|
|
|
第五章:域的扩张 |
7 |
6 |
|
|
1 |
|
|
|
合 计 |
34 |
29 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、考核说明
本课程采用期末考试与平时测评相结合;期末考试为闭卷考试,考试时间为120分钟;平时测评包括作业、期中考核等。学生修完本课程并参加考试后,其成绩的评定为:期末考试成绩(70%)+作业成绩(10%)+期中考核成绩(20%)。
六、主要教材及教学参考书目
(一)主要教材
1.韩士安,林磊著《近世代数》,高等教育出版社,2004年。
(二)主要参考书目
1.朱平天等著《近世代数》,科学出版社,2001年。